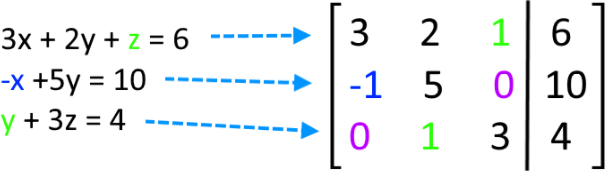
概率论与数理统计

概率论

自然界与社会生活中的两类现象

• 确定性现象：结果确定
• 不确定性现象：结果不确定

概率论与数理统计是研究随机现象统计规律的数学学科

随机事件的关系即运算

随机现象是在个别实验中结果呈现不确定性，但在大量重复试验中，其结果又具有统计规律的现象。

为了研究随机现象，就要对客观事件进行观察。观察随机现象的过程称为随机试验，简称试验。

随机试验的特点：

1. 在相同的条件下，试验可以重复进行。
2. 每一次试验的可能的结果不止一个（至少两个，也可以是无穷多个），并且能事先明确试验的所有可能结果。
3. 在每次试验之前不能确定哪一个结果会出现。

样本空间：随机试验 $E$ 的所有可能的结果组成的集合。记为 $S$（或 $\Omega$）

样本点：样本空间的元素，即 $E$ 的每一个结果。

随机试验 $E$ 的样本空间 $S$ 的子集 $A$ 称为 $E$ 的 随机事件，简称事件。

当 $A$ 中某一个样本点出现时，就说事件 $A$ 发生了。

由一个样本点 $e$ 组成的单点集 $\{e\}$ 称为基本事件。

由若干个基本事件组合而成的事件称为复合事件。

样本空间 $S$ 包含了试验的所有样本点，在每次试验中它总会发生，称 $S$ 是必然事件。

• 事件的包含：事件 $A$ 的发生必然导致事件 $B$ 发生，即属于 $A$ 的样本点也属于 $B$。
  • 称事件 $B$ 包含事件 $A$，或称事件 $A$ 包含于 $B$，记作 $B \supset A$ 或 $A \subset B$。

对任何事件 $A$，都有 $\varnothing \subset A \subset S$

• 事件的相等：如果事件 $A$ 包含事件 $B$（$A \supset B$），事件 $B$ 包含事件 $A$（$A \subset B$），即 $A$ 与 $B$ 有相同的样本点。
  • 称事件 $A$ 与事件 $B$ 相等，记作 $A=B$。

事件的并（和）可以推广到有限或可列个事件。

$n$ 个事件 $A_1, A_2, \ldots, A_n$ 中至少有一个发生的事件称为这些事件的和事件。

记作 $A_1 \cup A_2 \cup \ldots \cup A_n=\bigcup_{k=1}^n A_k$ 或 $A_1+A_2+\ldots+A_n=\sum_{k=1}^n A_k$

可列个事件 $A_1, A_2, \ldots, A_n, \ldots$ 中至少有一个发生的事件称为这些事件的和事件。

记作 $\bigcup_{k=1}^{\infty} A_k$或$\sum_{k=1}^{\infty} A_k$

• 事件的交（积）：两个事件 $A$ 与 $B$ 同时发生的事件。
  • 称事件 $A$ 与事件 $B$ 的交（积），记作 $A \cap B$ 或 $AB$
  • $A \cap B=\{x \mid x \in A$ 且 $x \in B\}$

事件的交（积）可以推广到有限或可列个事件。

$n$ 个事件$A_1, A_2, \ldots, A_n$ 中同时发生的事件称为这些事件的积事件。

记作 $A_1 \cap A_2 \cap \ldots \cap A_n=\bigcap_{k=1}^n A_k$ 或 $A_1 A_2 \cdots A_n$

可列个事件 $A_1, A_2, \ldots, A_n, \ldots$ 中同时发生的的事件称为这些事件的积事件。

记作 $\bigcap_{k=1}^{\infty} A_k$

• 对立事件/互逆事件：事件 $A$ 与事件 $B$ 必有一个发生，但又不能同时发生。

  • 称事件 $A$ 与事件 $B$ 为对立事件，也称 $A$ 与 $B$ 为互逆。
  • 事件 $A$ 的对立事件（逆事件）叫”$A$ 逆，非 $A$”，记作 $\bar{A}$
  • $\bar{A}=\{x \in S \mid x \notin A\}$

• 事件的差：事件 $A$ 发生，而事件 $B$ 不发生的事件。

  • 称为事件 $A$ 与事件 $B$ 的差，记作 $A-B$
  • $A-B=\{x \mid x \in A$ 且 $x \notin B\}$

• 互不相容事件/互斥事件：事件 $A$ 与事件 $B$ 不能同时发生。

  • 称事件 $A$ 与事件 $B$ 为互不相容事件，也称 $A$ 与 $B$ 为互斥。
  • $A B=\varnothing$

完备事件组：如果事件 $A_1, \ldots, A_n$ 两两互不相容，并且 $A_1 \cup \ldots \cup A_n=S$，则称 $A_1, \ldots, A_n$ 是一个完备事件组。

事件的运算本质就是集合的运算。

设 $A, B, C$ 为事件，则有：

1. 交换律

   1. $A \cup B=B \cup A$ 或 $A+B=B+A$
   2. $A \cap B=B \cap A$ 或 $A B=B A$

2. 结合律

   1. $A \cup(B \cup C)=(A \cup B) \cup C=A \cup B \cup C$ 或 $A+(B+C)=(A+B)+C=A+B+C$
   2. $A \cap(B \cap C)=(A \cap B) \cap C=A \cap B \cap C$ 或 $A(B C)=(A B) C=A B C$

3. 分配率

   1. $A \cup(B \cap C)=(A \cup B) \cap(A \cup C)$ 或 $A+B C=(A+B)(A+C)$
   2. $A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$ 或 $A(B+C)=A B+A C$

4. 德摩根律

   1. $\overline{A \cup B}=\bar{A} \cap \bar{B}$ 或 $\overline{A+B}=\bar{A} \bar{B}$
   2. $\overline{A \cap B}=\bar{A} \cup \bar{B}$ 或 $\overline{A B}=\bar{A}+\bar{B}$

   可以推广到有限个和可列个事件。

   $\overline{\bigcup_{i \in I} A_i} \equiv \bigcap_{i \in I} \overline{A_i}$
   $\overline{\bigcap_{i \in I} A_i} \equiv \bigcup_{i \in I} \overline{A_i}$

5. 其他运算律

   1. 等幂律：$A \cup A=A$ $\quad A +A=A$ $\quad A \cap A=A \quad A A=A$
   2. 0-1律：$\begin{array}{ll}A \cup S=S & A+S=S \\ A \cap S=A & A S=A \\ A \cup \varnothing=A & A+\varnothing=A \\ A \cap \varnothing=\varnothing & A \varnothing=\varnothing\end{array}$
   3. 吸收律：若$A \subset B$，则$A \cup B=B$$\quad A \cap B=A$
   4. 互补律：$A \cap \bar{A}=A \bar{A}=\varnothing$$ \quad A \cup \bar{A}=A+\bar{A}=S$
   5. 双重否定律：$\bar{\bar{A}}=A$

概率的定义即性质

（一）频率

​ 概率论研究的是随机现象的统计规律性。因此，仅仅知道试验中可能出现哪些事件是不够的，还必须对事件发生的可能性大小进行量的描述，也就是用一个实数来描述某个事件在一次试验中发生的可能性大小。

频率是描述事件发生的频繁程度的一个量。

• 随机事件在一次试验中是否发生是不确定的，但在大量重复的试验中，该事件的发生往往具有统计规律性。所以，我们可以用大量重复试验来研究该事件发生的可能性大小。
• 仅从事件出现的次数不能确切地描述该事件出现的可能性的大小，还应该考虑该事件出现次数在试验总次数中所占的百分比。

设在相同的条件下，进行了 $n$ 次试验，在这 $n$ 次试验中，事件 $A$ 发生的次数称为事件 $A$ 发生的频数，记作 $n(A)$。比值 $n(A) / n$ 称为事件 $A$ 的频率，记作 $f_n(A)$。即 $f_n(A)=\frac{n(A)}{n}$。

基本性质：

• 非负性：$0 \leq f_n(A) \leq 1$

• 规范性：$f_n(\varnothing)=0$，$f_n(S)=1$

• 可加性：设 $A$，$B$ 互不相容，则 $f_n(A \cup B)=f_n(A)+f_n(B)$

  设 $A_1, A_2, \ldots, A_k$ 互不相容，则 $f_n\left(A_1 \cup A_2 \cup \ldots \cup A_k\right)=f_n\left(A_1\right)+f_n\left(A_2\right)+\ldots+f_n\left(A_k\right)$

（二）概率

随着 $n$ 的增大，事件 $A$ 的频率 $f_n(A)$ 呈现出稳定性。即频率会逐渐稳定与一个介于 $0$ 和 $1$ 之间的常数。因此，我们可以让重复试验次数 $n$ 增大，观察频率 $f_n(A)$ 的稳定值，并用这个值来表征事件 $A$ 发生的可能性的大小：概率的统计定义。

概率的统计定义：事件 $A$ 发生的频率的稳定值 $p$ 称为 $A$ 的统计概率，记作 $P(A)$，即 $P(A)=p$。

当试验次数 $n$ 相当大时，可以用频率作为概率的近似值：$P(A) \approx f_n(A)=\frac{n(A)}{n}$

但是在实际问题中，我们不可能对每一个事件都通过做大量的试验来求得事件的频率，并用来表示该事件发生可能性的大小。同时，为了理论研究的需要，我们需要将事件发生的可能性给出一个数学上的定义。为此，我们从频率的稳定性和频率的性质得到启发，给出表征事件发生可能性大小的概率的定义：概率的公理化定义。

概率的公理化定义：设 $E$ 是随机试验，$S$ 是它的样本空间。对 $E$ 的每一个事件 $A$ 赋予一个实数，记作 $P(A)$，称为事件 $A$ 的公理化概率。

函数 $P(A)$ 满足下列条件：

1. 非负性：对每一个事件 $A$，有 $P(A)≥0$。
2. 规范性：对于必然事件 $S$，有 $P(S)=1$。
3. 可列可加性：对于两两互不相容的事件 $A_1, A_2, \ldots$，有 $P\left(A_1 \cup A_2 \cup \ldots\right)=P\left(A_1\right)+P\left(A_2\right)+\ldots$，即 $P\left(\bigcup_{i=1}^{\infty} A_i\right)=\sum_{i=1}^{\infty} P\left(A_i\right)$

==概率的本质：概率$P$是定义在事件集合上的满足以上三个条件的实函数：$P:\{$ 事件 $\} \rightarrow R$==

（三）概率的性质

1. $P(\varnothing)=0$
2. 有限可加性， 设 $A_1, A_2, \ldots, A_n$ 是两两互不相容的事件, 则有 $P\left(A_1 \cup A_2 \cup \ldots \cup A_n\right)=P\left(A_1\right)+P\left(A_2\right)+\ldots+P\left(A_n\right)$
3. 设事件 $A$ 和$B$满足 $A \subset B$，则
   1. 单调性：$P(A) \leq P(B)$
   2. 减法公式：$P(B-A)=P(B)-P(A)$
4. 对任何事件 $A$，有 $0 \leq P(A) \leq 1$（任何事件都概率都介于 $0$ 和 $1$ 之间）
5. 逆事件的概率，对任何事件 $A$，有 $P(A)+P(\bar{A})=1$或$P(\bar{A})=1-P(A)$
6. 加法公式，对于任意两个事件 $A$ 和 $B$，有 $P(A \cup B)=P(A)+P(B)-P(A B)$

古典概型与几何概型

古典概型：

1. 试验的样本空间包含有限个元素
2. 试验中每个基本事件发生的可能性相同

具有以上两个特点的试验大量存在。这种试验称为等可能概型。它在概率论发展初期曾经是主要研究对象，所以也称为古典概型。

设 $E$ 是一个有 $n$ 个基本事件的等可能概型：$S=\left\{e_1, e_2, \ldots, e_n\right\}$，由于在试验中每一个基本事件 $e_i$
发生的可能性（概率）相同：

$P\left(\left\{e_i\right\}\right)=\frac{1}{n}(i=1,2, \ldots, n)$

设事件$A$有$k$个基本事件组成：$A=\left\{e_{i_1}, e_{i_2}, \ldots, e_{i_k}\right\}$，则 $A$ 的概率：

P(A)=P\left(\left\{e_{i_1}, e_{i_2}, \ldots, e_{i_k}\right\}=P\left(\left\{e_{i_1}\right\} \cup\left\{e_{i_2}\right\} \cup \ldots \cup\left\{e_{i_k}\right\}\right)\right.=P\left(\left\{e_{i_1}\right\}\right)+P\left\{\left\{e_{i_2}\right\}\right\}+\ldots+P\left(\left\{e_{i_k}\right\}\right)=\frac{1}{n}+\frac{1}{n}+\ldots+\frac{1}{n}=\frac{k}{n}$​

几何概型：设试验的样本空间为一几何区域，其测度（长度、面积或体积等） 为有限值，若任意事件发生的概率与的测度成正比，则称该试验为几何概型。

条件概率与乘法公式

设 $A$，$B$ 是两个事件，且 $p(A)>0$，称 $\frac{P(A B)}{P(A)}$ 为在事件 $A$ 发生的条件下事件 $B$ 发生的条件概率，记作 $P(B \mid A)$，即$P(B \mid A)=\frac{P(A B)}{P(A)}$.

1. 非负性，对任何事件 $B$，$P(B \mid A)=\frac{P(A B)}{P(A)} \geq 0$
2. 规范性，对必然事件 $S$，$P(S \mid A)=\frac{P(A S)}{P(A)}=\frac{P(A)}{P(A)}=1$
3. 可列可加性，设 $B_1, B_2, \ldots$ 两两互不相容

$P\left(\bigcup_{i=1}^{\infty} B_i \mid A\right)=\frac{P\left[A\left(\bigcup_{i=1}^{\infty} B_i\right)\right]}{P(A)}=\frac{P\left(\bigcup_{i=1}^{\infty} A B_i\right)}{P(A)}=\frac{\sum_{i=1}^{\infty} P\left(A B_i\right)}{P(A)}=\sum_{i=1}^{\infty} \frac{P\left(A B_i\right)}{P(A)}=\sum_{i=1}^{\infty} P\left(B_i \mid A\right)$

乘法公式：$P(A B)=P(A) P(B \mid A) \quad(P(A)>0)$

推广：$P(A B C)=P(A) P(B \mid A) P(C \mid A B) \quad(P(A B)>0)$

更加一般的：

$\begin{aligned} P\left(A_1 A_2 A_3 \cdots A_n\right)=P\left(A_1\right) & P\left(A_2 \mid A_1\right) P\left(A_3 \mid A_1 A_2\right) \cdots P\left(A_n \mid A_1 A_2 \cdots A_{n-1}\right) & \left(P\left(A_1 A_2 \cdots A_{n-1} A_n\right)>0\right)\end{aligned}$

全概率公式与贝叶斯公式

【定理】设试验 $E$ 的样本空间为 $B_1, B_2, \ldots, B_n$，为 $S$ 的一个划分（完备事件组），且 $P\left(B_i\right)>0$（$i=1,2, \ldots, n$），$A$ 为 $E$ 的一个事件，则

$\begin{aligned} P(A)= & P\left(B_1\right) P\left(A \mid B_1\right)+P\left(B_2\right) P\left(A \mid B_2\right) \left.+\ldots+P\left(B_n\right) P\left(A \mid B_n\right)\right)=\sum_{i=1}^n P\left(B_i\right) P\left(A \mid B_i\right)\end{aligned}$

意义：事件 $A$ 的发生有各种可能的原因 $B_i$（$i=1,...n$）。如果 $A$ 是由原因$B_i$引起，则 $A$ 发生的概率为 $P\left(A B_i\right)=P\left(B_i\right) P\left(A \mid B_i\right)$。每一个原因都可能导致 $A$ 发生，故 $A$ 发生的概率是全部原因引起 $A$ 发生的概率的总和，即为全概率公式。

由此可以形象地把全概率公式看成是“==由原因推结果==”的公式。

【定理】设试验 $E$ 的样本空间为 $S$，$B_1, B_2...B_n$ 为 $S$ 的一个划分（完备事件组）且 $P(B_i)>0$（$i=1,2,..n$），$A$ 为 $E$ 的一个事件，且 $P(A)>0$，则

$P\left(B_i \mid A\right)=\frac{P\left(B_i\right) P\left(A \mid B_i\right)}{\sum_{j=1}^n P\left(B_j\right) P\left(A \mid B_j\right)}(i=1,2, \ldots, n)$

意义：在事件 $A$ 已经发生的条件下，贝叶斯公式可用来寻找导致 $A$ 发生各种原因 $B_i$ 的概率。

由此可以形象地把贝叶斯公式看成是“==由结果推原因==”的公式。

事件的独立性

设 $A$，$B$ 是两个事件，如果它们满足等式 $P(AB)=P(A)P(B)$ 则称事件 $A$ 与$B$相互独立，简称$A$，$B$ 独立。

一维随机变量

一维随机变量：随机变量 $X$ 定义在随机试验样本空间 $S=\{e\}$ 上的单实值函数，记为

$X=X(e)$

一维离散型随机变量

一维离散型随机变量：随机变量的全部可能取值是有限个或可列无限个。可列无限个是指能与自然数一一对应上。

一维离散型随机变量的分布律：设离散型随机变量 $X$ 的所有可能取值为 $x_k \ (k=1,2,\cdots)$，$X$ 取到各个可能值的概率 $P\left(X=x_k\right)=p_k \ (k=1,2,3, \cdots)$，称为随机变量 $X$ 的概率分布。

$\begin{array}{l|l|l|l|l|l|l} X & x_1 & x_2 & x_3 & \cdots & x_n & \ldots \\ \hline p_k & p_1 & p_2 & p_3 & \cdots & p_n & \cdots \end{array}$

注

1. $p_k \geq 0,(k=1,2, \cdots)$
2. $\sum_{k=1}^{+\infty} p_k=1$

常见的一维离散型随机变量：

$0-1$ 分布：随机试验的结果只有两个，一维离散随机变量 $X$ 的取值是 $0$ 和 $1$，对应的分布律

$\begin{array}{c|c|c} X & 0 & 1 \\ \hline p_k & 1-p & p \end{array}$

二项分布：只有两个结果的随机试验称为伯努利试验，观察 $A$ 发生或 $A$ 不发生，试验进行 $n$ 次，称为 $n$ 重伯努利试验。随机变量 $X$ 的取值是 $n$ 重伯努利试验中 $A$ 发生的次数。假设单独一次试验 $A$ 发生的概率为 $p(0<p<1)$，$A$ 不发生的概率为 $q(q=1-p)$，则 $n$ 次试验中 $A$ 发生 $k$ 次的概率为：

$P(X=k)=C_n^k p^k q^{n-k} \quad (k=0,1,2, \cdots)$

记为 $X \sim B(n,p)$。

泊松分布：对应的分布律

$P(X=k)=\frac{\lambda^k e^{-\lambda}}{k !} \quad (k=0,1,2, \cdots)$

$\lambda >0$，表示单位时间（空间）内随机事件发生的平均次数。

记为 $X \sim P(\lambda)$。

泊松定理：设 $\lambda >0$，$n$ 是任意正整数，设 $np_n=\lambda$，则对任一固定的非负整数 $k$，有

$\lim _{n \rightarrow \infty} C_n^k p_n^k\left(1-p_n\right)^{n-k}=\frac{\lambda^k e^{-\lambda}}{k !}$

如果 $X \sim B(n,p)$，且 $n$ 很大，$p$ 很小时，$X \sim P(\lambda=np)$

$P(X=k)=C_n^k p^k(1-p)^{n-k} \approx \frac{(n p)^k e^{-n}}{k !}$

一维随机变量的分布函数：设 $X$ 是随机变量，$x$ 是任意实数，$F(x)$ 记为 $X$ 的分布函数。满足

$F(x)=P(X \leq x) \quad -\infty<x<+\infty$

注：

1. $F(x)$ 是一个不减函数
2. $P(a<X \leq b)=F(b)-F(a)$
3. $0 \leq F(x) \leq 1, F(-\infty)=0, F(+\infty)=1$
4. $F(x)$ 右连续

一维连续型随机变量

一维连续型随机变量：设 $X$ 是随机变量，$x$ 是任意实数，$F(x)$ 是 $X$ 的分布函数，存在非负可积函数 $f(x)$ ，使对于任意实数 $x$ 有

$F(x)=\int_{-\infty}^x f(t) d t$

则称 $X$ 为一维连续型随机变量，$f(x)$ 为 $X$ 的概率密度函数。

注：

1. $f(x) \geqslant 0$
2. $\int_{-\infty}^{+\infty} f(x) d x=1$
3. $P\left(x_1<X \leq x_2\right)=F\left(x_2\right)-F\left(x_1\right)=\int_{x_1}^{x_2} f(x) d x$
4. $P\left(x_1<X \leq x_2\right)=P\left(x_1 \leq X \leq x_2\right)=P\left(x_1 \leq X<x_2\right)=P\left(x_1<X<x_2\right)$
5. 若 $f(x)$ 在点 $x$ 出连续，则有 $F^{\prime}(x)=f(x)$

常见的一维连续型随机变量：

均匀分布：若一维连续型随机变量 $X$ 具有概率密度

$f(x)=\left\{\begin{array}{cc} \frac{1}{b-a}, & a<x<b \\ 0, & \text { 其他 } \end{array}\right.$

则称 $X$ 在区间 $(a,b)$ 上服从均匀分布，记为 $X \sim U(a, b)$。

$X$ 的分布函数 $F(x)$：

$F(x)=\left\{\begin{array}{cc} 0, & x<a \\ \frac{x-a}{b-a}, & a \leq x<b \\ 1, & x \geq b \end{array}\right.$

指数分布：若一维连续型随机变量 $X$ 具有概率密度

$f(x)=\left\{\begin{array}{cc} \lambda e^{-\lambda x}, & x>0 \\ 0, & \text { 其他 } \end{array}\right.$

其中 $\lambda>0$，则称 $X$ 在服从参数为 $\lambda$ 的指数分布，记为 $X \sim E(\lambda)$。

$X$ 的分布函数 $F(x)$：

$F(x)=\left\{\begin{array}{cc} 1-e^{-\lambda x}, & x>0 \\ 0, & \text { 其他 } \end{array}\right.$

指数分布的无记忆性：对于任意的 $s, t>0$，有 $P(X>s+t \mid X>s)=P(X>t)$

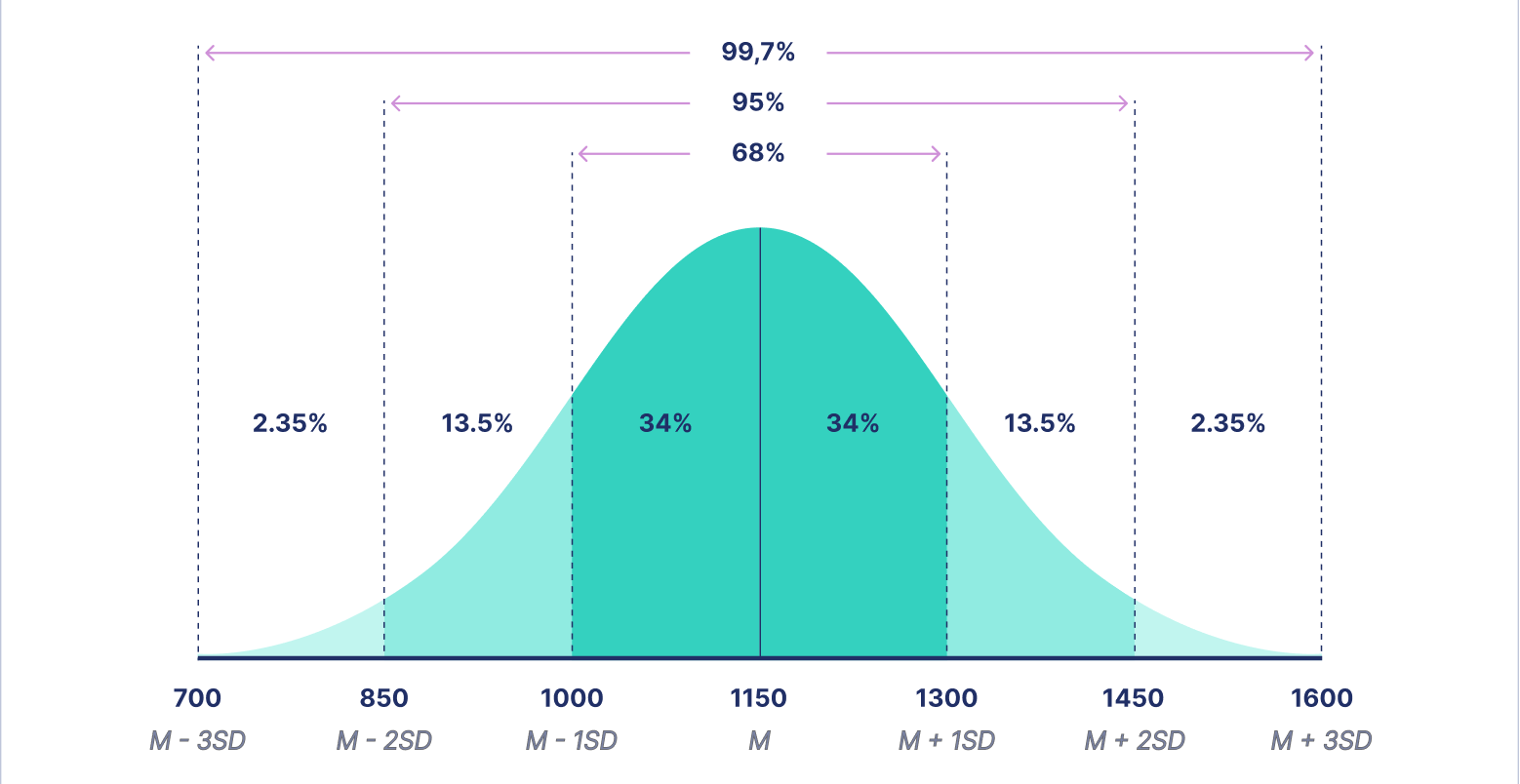
正态分布/常态分布/高斯分布：若一维连续型随机变量 $X$ 具有概率密度

$\varphi(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} \quad \left(-\infty<x<+\infty\right)$

其中 $\mu, \sigma(\sigma>0)$，则称 $X$ 在服从参数为 $\mu$，$\sigma$ 的正态分布，记为 $X \sim N\left(\mu, \sigma^2\right)$。

 

标准正态分布：$X \sim N\left(0, 1\right)$

$f(x)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} \quad -\infty<x<+\infty$

注：

1. 概率密度 $f(x)$ 关于 $x=0$ 对称
2. 分布函数 $\Phi(-x)=1-\Phi(x)$
3. 若 $X \sim N\left(\mu, \sigma^2\right)$，则 $Z=\frac{X-\mu}{\sigma} \sim N(0,1)$

$F(x)=P(X \leq x)=P\left(\frac{X-\mu}{\sigma} \leq \frac{x-\mu}{\sigma}\right)=P\left(Z \leq \frac{x-\mu}{\sigma}\right)=\Phi\left(\frac{x-\mu}{\sigma}\right)$

$P\left(x_1<X<x_2\right)=P\left(\frac{x_1-\mu}{\sigma}<\frac{X-\mu}{\sigma} \leq \frac{x_2-\mu}{\sigma}\right)=\Phi\left(\frac{x_2-\mu}{\sigma}\right)-\Phi\left(\frac{x_1-\mu}{\sigma}\right)$

$P(X \geq x)=1-P(X<x)=1-P\left(\frac{X-\mu}{\sigma}<\frac{x-\mu}{\sigma}\right)=1-\Phi\left(\frac{x-\mu}{\sigma}\right)$

一维随机变量函数的分布

二维随机变量

二维离散型随机变量

二维随机变量：设 $E$ 是一个随机试验，其样本空间为 $S=\{e\}$，设 $X=X(e)$，$Y=Y(e)$ 是定义在样本空间上的随机变量，则由它们构成的向量 $(X,Y)$，称二维随机向量，或二维随机变量。

二维离散型随机变量：对应

• 联合分布律：

$P\left\{X=x_i, Y=y_j\right\}=p_i \quad (i, j=1,2, \cdots)$

注：

1. $p_{i j} \geq 0$
2. $\sum_i \sum_j p_{i j}=1$

• 联合分布函数：

$F(x, y)=P\{X \leq x, Y \leq y\}=\sum_{x_i \leq x, y \leq y} \sum_y p_y \quad (i, j=1,2, \cdots)$

边缘分布：单独考虑随机变量 $X$ 或随机变量 $Y$ 的分布情况

• 随机变量 $X$ 的边缘分布

$P_{i \cdot}=\sum_j p_i \quad (j=1,2, \cdots)$

$F_X(x)=P\{X \leq x\}$

• 随机变量 $Y$ 的边缘分布

$P_{\cdot j}=\sum_i p_j \quad (i=1,2, \cdots)$

$F_Y(y)=P\{Y \leq y\}$

条件分布

独立性：关心两个随机变量之间是否存在某种依赖关系。对于二维随机变量 $X$，$Y$ 相互独立

$\Leftrightarrow$ $P_{i j}=P_{i \cdot} \times P_{\cdot j} \quad (i, j=1,2, \cdots)$

$\Leftrightarrow$ $F(x, y)=F_X(x) \cdot F_Y(y)$

二维连续型随机变量

联合概率密度：$f(x,y)$

联合概率分布函数：$F(x,y)$

$F(x, y)=P\{X \leq x, Y \leq y\}=\int_{-\infty}^y \int_{-\infty}^x f(u, v) d u d v$

注：

1. $f(x, y) \geq 0$
2. $\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) d x d y=F(+\infty,+\infty)=1$
3. 设 $G$ 是 $xOy$ 平面上的区域，则点 $X,Y$ 落在 $G$ 内的概率：

$\iint_G f(x, y) d x d y$

$P\{a<x<b, c<y<d\}=\int_c^d \int_a^b f(x, y) d x d y$

4. 若 $f(x,y)$ 在点 $(x,y)$ 处连续，则有 $\frac{\partial^2 F(x, y)}{\partial x \partial y}=f(x, y)$

边缘分布：单独考虑随机变量 $X$ 或随机变量 $Y$ 的分布情况

• 随机变量 $X$ 的边缘分布

$f_X(x)=\left[F_X(x)\right]^{\prime}=\int_{-\infty}^{+\infty} f(x, y) d y$

$F_X(x)=F(x,+\infty)=\int_{-\infty}^x\left[\int_{-\infty}^{+\infty} f(x, y) d y\right] d x$

• 随机变量 $Y$ 的边缘分布

$f_Y(y)=\left[F_Y(y)\right]^{\prime}=\int_{-\infty}^{+\infty} f(x, y) d x$

$F_Y(y)=F(+\infty, y)=\int_{-\infty}^y\left[\int_{-\infty}^{+\infty} f(x, y) d x\right] d y$

条件分布：

对于 $f_Y(y)>0$，

$f_{X \mid Y}(X=x \mid Y=y)=\frac{f(x, y)}{f_Y(y)}$

对于 $f_X(x)>0$，

$f_{Y \mid X}(Y=y \mid X=x)=\frac{f(x, y)}{f_X(x)}$

独立性：关心两个随机变量之间是否存在某种依赖关系。对于二维随机变量 $X$，$Y$ 相互独立

$f(x, y)=f_X(x) \cdot f_Y(y)$

常用的二维连续型随机变量分布：

二维连续型随机变量均匀分布：若二维连续型随机变量 $(X,Y)$ 具有概率密度

$f(x, y)=\left\{\begin{array}{cc} \frac{1}{A}, & (x, y) \in G \\ 0, & \text { 其他 } \end{array}\right.$

则称 $X$ 在平面有界区域 $G$（$G$ 的面积为 $A$） 上服从二维均匀分布

二维连续型随机变量正态分布：若二维连续型随机变量 $(X,Y)$ 具有概率密度

$f(x, y)=\frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} \exp \left\{-\frac{1}{2\left(1-\rho^2\right)}\left[\frac{\left(x-\mu_1\right)^2}{\sigma_1^2}-2 \rho \frac{\left(x-\mu_1\right)\left(y-\mu_2\right)}{\sigma_1 \sigma_2}+\frac{\left(y-\mu_2\right)^2}{\sigma_2^2}\right]\right\}$

其中 $(-\infty<x, y<+\infty)$，且 $\sigma_1>0$，$\sigma_2>0$，$-1<\rho<1$，则称 $(X,Y)$ 服从参数为 $\sigma_1, \sigma_2, \mu_1, \mu_2, \rho$ 的正态分布，记为 $(X, Y) \sim N\left(\mu_1, \sigma_1^2 ; \mu_1, \sigma_2^2 ;, \rho\right)$

特别地，当 $\mu_1=0$，$\mu_2=0$，$\sigma_1=1$，$\sigma_2=1$ 时，称 $(X,Y)$ 服从标准正态分布。

二维随机变量函数的分布

二维离散型随机变量函数的分布（忽略 $\cdots$）

二维连续型随机变量函数的分布：设二维连续型随机变量 $(X, Y)$，则 $Z=g(X, Y)$

$F_Z(z)=P\{Z \leq z\}=\iint_{g(x, y) \leq z} f(x, y) d x d y$

$f_z(z)=F_z^{\prime}(z)$

特殊类型：

• $Z=X+Y$

$f_Z(z)=\int_{-\infty}^{+\infty} f(x, z-x) d x=\int_{-\infty}^{+\infty} f(z-y, y) d y$

特别地，当 $X$，$Y$ 相互独立时，有

$f_Z(z)=\int_{-\infty}^{+\infty} f_X(x) f_Y(z-x) d x=\int_{-\infty}^{+\infty} f_X(z-y) f_Y(y) d y,$

• $\frac{Y}{X}$，$\frac{X}{Y}$

$f_Z(z)=\int_{-\infty}^{+\infty}|x| f(x, x z) d x=\int_{-\infty}^{+\infty}|y| f(y z, y) d y$

特别地，当 $X$，$Y$ 相互独立时，有

$f_Z(z)=\int_{-\infty}^{+\infty}|x| f_X(x) f_Y(x z) d x=\int_{-\infty}^{+\infty}|y| f_X(y z) f_Y(y) d y$

• $Z=XY$

$f_Z(z)=\int_{-\infty}^{+\infty} \frac{1}{|x|} f\left(x, \frac{z}{x}\right) d x .$

特别地，当 $X$，$Y$ 相互独立时，有

$f_Z(z)=\int_{-\infty}^{+\infty} \frac{1}{|x|} f_X(x) f_Y\left(\frac{z}{x}\right) d x$

• $Z=\max(X,Y)$，$Z=\min(X,Y)$

数学期望

随机变量的数学期望：随机变量有对应概率加权后的平均值。

• （一维）离散型随机变量的数学期望：设离散型随机变量 $X$ 的分布律为 $P\left\{X=x_i\right\}=p_i(i=1,2 \cdots)$，若级数 $\sum_{i=1}^{\infty} x_i p_i$ 绝对收敛，则称 $\sum_{i=1}^{\infty} x_i p_i$ 为离散型随机变量 $X$ 的数学期望，记为 $E(X)$，即 $E(X)=\sum_{i=1}^{\infty} x_i p_i$。

• （一维）连续型随机变量的数学期望：设连续型随机变量 $X$ 的概率密度为 $f(x)$，若积分 $\int_{-\infty}^{+\infty} x f(x) d x$ 绝对收敛，则称 $\int_{-\infty}^{+\infty} x f(x) d x$ 为 $X$ 的数学期望，记为 $E(X)$，即 $\int_{-\infty}^{+\infty} x f(x) d x$。

相关性质：设 $C$ 为常数

1. $E(C)=C$
2. $E(CX)=CE(X)$
3. $E(X+Y)=E(X)+E(Y)$
4. $E(a X \pm b Y)=a E(X) \pm b E(Y)$
5. 设 $X$ 与 $Y$ 相互独立，$E(XY)=E(X)E(Y)$（反之不成立）

随机变量函数的数学期望：

• 一维随机变量函数的数学期望：设 $X$ 是一个随机变量，$g(x)$ 为连续实函数，令 $Y=g(X)$

  • 若 $X$ 是一维离散型随机变量，分布律为 $P\left\{X=x_i\right\}=p_i(i=1,2 \cdots)$，若级数 $\sum_{i=1}^{\infty} g\left(x_i\right) p_i$ 绝对收敛，则称一维离散型随机变量 $Y=g(X)$ 的期望存在，且 $E(Y)=\sum_{i=1}^{\infty} g\left(x_i\right) p_i$
  • 若 $X$ 是一维连续型随机变量，概率密度为 $f(x)$，若积分 $\int_{-\infty}^{+\infty} g(x) f_X(x) d x$ 绝对收敛，则称一维连续型随机变量 $Y=g(X)$ 的期望存在，且 $E(Y)=\int_{-\infty}^{+\infty} g(x) f_X(x) d x$

• 二维随机变量函数的数学期望：设 $(X,Y)$ 为二维变量，$g(x,y)$ 为二元连续实函数，令 $Z=g(X,Y)$

  • 若 $(X,Y)$ 是二维离散型随机变量，联合分布律为 $P\left\{X=x_i, Y=y_j\right\}=p_y, i, j=1,2 \cdots$，若级数 $\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} g\left(x_i, y_i\right) p_y$ 绝对收敛，则称二维离散型随机变量 $Z=g(X,Y)$ 的期望存在，且 $E(Z)=E[g(X, Y)]=\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} g\left(x_i, y_j\right) p_{i j}$
  • 若 $(X,Y)$ 是二维连续型随机变量，联合密度为 $f(x,y)$，若积分 $\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} g(x, y) f(x, y) d x d y$ 绝对收敛，则称二维连续型随机变量 $Z=g(X,Y)$ 的期望存在，且 $E(Z)=E[g(X, Y)]=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} g(x, y) f(x, y) d x d y$

方差

方差：衡量随机变量平均偏离程度。

设 $X$ 是一个随机变量，如果 $E\left\{\left[X-E(X)\right]^2\right\}$ 存在，则称 $E\left\{\left[X-E(X)\right]^2\right\}$ 为 $X$ 的方差，记作 $D(X)$，即

$D(X)=E\left\{\left[X-E(X)\right]^2\right\}$

$\sqrt{D(X)}$ 为标准差或均方差。

$D(X)=E\left(X^2\right)-[E(X)]^2$

相关性质：设 $C$ 为常数

1. $D(C)=0$
2. $D(CX)=C^2D(X)$
3. $D(X+C)=D(X)$
4. 设 $X$ 与 $Y$ 相互独立，
   1. $D(X \pm Y)=D(X)+D(Y)$
   2. $D(a X \pm b Y)=a^2 D(X) + b^2 D(Y)$

常用随机变量数学期望和方差

分布	参数	分布律/概率密度	数学期望	方差
$0-1$ 分布	$p$	$P\{x=k\}=p^k(1-p)^{1-k} \quad (k=0,1)$	$p$	$p(1-p)$
二项分布 $B(n,p)$	$n,p$	$P\{x=k\}=C_n^k p^k(1-p)^{1-k} \quad (k=0,1,\cdots,n)$	$np$	$np(1-p)$
泊松分布 $P(\lambda)$	$\lambda$	$P\{x=k\}=\frac{\lambda^k e^{-\lambda}}{k !}$	$\lambda$	$\lambda$
均匀分布 $U(a,b)$	$a<b$	$f(x)=\frac{1}{b-a},(a<x<b)$	$\frac{a+b}{2}$	$\frac{(b-a)^2}{12}$
正态分布 $N\left(\mu, \sigma^2\right)$	$\mu, \sigma$	$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}$	$\mu$	$\sigma^2$
指数分布 $e(\lambda)$	$\lambda$	$f(x)=\left\{\begin{array}{cc}\lambda e^{-\lambda x}, & x>0 \\ 0, & \text { 其他 }\end{array}\right.$	$\frac{1}{\lambda}$	$\frac{1}{\lambda^2}$

协方差

协方差：设 $(X,Y)$ 是二维随机变量，且 $E(X)$ 和 $E(Y)$ 都存在，如果 $E[(X-E(X))(Y-E(Y))]$ 存在，则称 $E[(X-E(X))(Y-E(Y))]$ 为 $X$ 和 $Y$ 的协方差，记作 $\operatorname{Cov}(X,Y)$，即

$\operatorname{Cov}(X, Y)=E[(X-E(X))(Y-E(Y))]$

$\operatorname{Cov}(X, Y)=E(X Y)-E(X) E(Y)$

相关性质：设 $C$ 为常数

1. $\operatorname{Cov}(X, Y)=\operatorname{Cov}(Y, X)$
2. $\operatorname{Cov}(X, Y+Z)=\operatorname{Cov}(X, Y)+\operatorname{Cov}(X, Z)$
3. $\operatorname{Cov}(a X, b Y)=a b \operatorname{Cov}(X, Y)$
4. $\operatorname{Cov}\left(a X_1 \pm b X_2, Y\right)=a \operatorname{Cov}\left(X_1, Y\right) \pm b \operatorname{Cov}\left(X_2, Y\right)$
5. $\operatorname{Cov}(C, X)=0$
6. $D(X \pm Y)=D(X)+D(Y) \pm 2\operatorname{Cov}(X, Y)$
7. 设 $X$ 与 $Y$ 相互独立，$\operatorname{Cov}(X, Y)=0$

相关系数

相关系数：设 $(X,Y)$ 是二维随机变量，且 $D(X)$ 和 $D(Y)$ 都存在，且都不为零，则称 $\rho_{X Y}=\frac{\operatorname{cov}(X, Y)}{\sqrt{D X} \sqrt{D Y}}$ 为 $X$ 与 $Y$ 的相关系数。

相关性质：设 $C$ 为常数

1. $\left|\rho_{X Y}\right| \leq 1$
2. 当 $\left|\rho_{X Y}\right|=0$，称 $X$ 与 $Y$ 不相关
3. $X$ 和 $Y$ 相互独立则 $X$ 和 $Y$ 不相关，反之不一定

大数定理及中心极限定理

切比雪夫不等式：设随机变量 $X$，其 $E(X)=\mu$，$D(X)=\sigma^2$ 都存在，则对于任意 $\varepsilon>0$ 均有：

$P\{|X-E(X)| \geq \varepsilon\} \leq \frac{D(X)}{\varepsilon^2}$

$P\{|X-E(X)|<\varepsilon\} \geq 1-\frac{D(X)}{\varepsilon^2}$

大数定律：依概率收敛指有 $X_1, X_2, \cdots X_n, \cdots$ 随机变量序列，$a$ 是常数，如果对于任意给定的正数 $\varepsilon$，有：

$\lim _{n \rightarrow \infty} P\left\{X_n-a \mid<\varepsilon\right\}=1$

则称随机变量序列 $X_1, X_2, \cdots X_n, \cdots$ 依概率收敛于 $a$，记为 $X_n \stackrel{P}{\longrightarrow} a$

切比雪夫大数定理：设 $X_1, X_2, \cdots X_n, \cdots$ 随机变量序列互不相干，且数学期望存在，又存在常数 $C>0$，使 $D\left(X_i\right) \leq C(i=1,2, \cdots)$，则对任意 $\varepsilon>0$，有：

$\lim _{n \rightarrow \infty} P\left\{\left|\frac{1}{n} \sum_{i=1}^n X_i-\frac{1}{n} \sum_{i=1}^n E\left(X_i\right)\right|<\varepsilon\right\}=1$

在定理条件下，有：

$\frac{1}{n} \sum_{i=1}^n X_i-\frac{1}{n} \sum_{i=1}^n E\left(X_i\right) \stackrel{P}{\longrightarrow} 0$

辛钦大数定律：设 $X_1, X_2, \cdots X_n, \cdots$ 随机变量序列独立同分布，且数学期望存在，则对任意 $\varepsilon>0$，有：

$\lim _{n \rightarrow \infty} P\left\{\left|\frac{1}{n} \sum_{i=1}^n X_i-\mu\right|<\varepsilon\right\}=1$

在定理条件下，有：

$\frac{1}{n} \sum_{i=1}^n X_i \rightarrow \mu$

伯努利大数定理：设 $\mu_n$ 是 $n$ 次独立试验中事件 $A$ 发生的次数，$p$ 是事件 $A$ 在每次试验中发生的概率，则对任意 $\varepsilon>0$，有：

$\lim _{n \rightarrow \infty} P\left\{\left|\frac{\mu_n}{n}-p\right|<\varepsilon\right\}=1$

事件 $A$ 发生的频率依概率收敛于事件 $A$ 发生的概率：

$\frac{\mu_n}{n} \stackrel{p}{\longrightarrow} p$

中心极限定理：

林德伯格-莱维中心极限定理：设 $X_1, X_2, \cdots X_n, \cdots$ 随机变量序列独立同分布，且期望和方差均存在，即 $E\left(X_k\right)=\mu$，$D\left(X_k\right)=\sigma^2>0 \quad (k=1,2,3, \cdots)$ ，则随机变量之和 $\sum_{i=1}^n X_k$ 的标准化变量：

$Y_n=\frac{\sum_{k=1}^n X_k-E\left(\sum_{k=1}^n X_k\right)}{\sqrt{D\left(\sum_{k=1}^n X_k\right)}}=\frac{\sum_{k=1}^n X_k-n \mu}{\sqrt{n} \sigma}$

的分布函数 $F_n(x)$ 对于任意 $x$ 满足：

$\lim _{n \rightarrow \infty} F_n(x)=\lim _{n \rightarrow \infty} P\left\{\frac{\sum_{k=1}^n X_k-n \mu}{\sqrt{n} \sigma} \leq x\right\}=\int_{-\infty}^x \frac{1}{\sqrt{2 \pi}} e^{-\frac{r^2}{2}} d t=\Phi(x)$

迪莫夫-拉普拉斯中心极限定理：设 $X_1, X_2, \cdots X_n, \cdots$ 随机变量序列独立同分布，且都服从 $0-1$ 分布，即 $P\left(X_k=1\right)=p$，$P\left(X_k=0\right)=1-p \quad (0<p<1, k=1,2,3, \cdots)$，则随机变量之和 $\sum_{i=1}^n X_k$ 的分布函数 $F_n(x)$ 对于任意 $x$ 满足：

$\lim _{n \rightarrow \infty} F_n(x)=\lim _{n \rightarrow \infty} P\left\{\frac{\sum_{k=1}^n X_k-n p}{\sqrt{n p(1-p)}} \leq x\right\}=\int_{-\infty}^x \frac{1}{\sqrt{2 \pi}} e^{\frac{t^2}{2}} d t=\Phi(x)$

数理统计

科学研究有两种逻辑思维：

演绎法（deduction）：从一条公理触发进行推演分析。

归纳法（induction）：从大量经验事实中总结出最接近本质的原理。

数理统计工作分类：

1. 收集整理数据资料，并展示数据（描述统计）
2. 对数据进行分析，从而对观察对象的性质特点做出推断（统计推断）

抽样分布

总体：试验的全部可能观察值。

个体：每一个可能的观察值。

总体容量：总体中包含的个体数量。

抽样调查：从总体中随机抽取一部分个体观测结果。

随机样本/样本：设 $X$ 是具有分布函数 $F$ 的随机变量，若 $X_1, X_2, \cdots, X_n$ 是与 $X$ 具有同一分布函数 $F$ 且相互独立的随机变量，则称 $X_1, X_2, \cdots, X_n$ 为从总体 $X$ 得到的容量为 $n$ 的简单随机样本，简称样本，观测值 $x_1, x_2, \cdots, x_n$ 称为样本值。

统计量：设 $X_1, X_2, \cdots, X_n$ 是来自总体 $X$ 的一个样本, $g\left(X_1, X_2, \cdots, X_n\right)$ 是 $X_1, X_2, \cdots, X_n$ 的函数， 若 $g$ 中不含有未知的参数, 则称 $g\left(X_1, X_2, \cdots, X_n\right)$ 是一个统计量。

常用统计量

名称	定义
样本均值	$\bar{X}=\frac{1}{n}\left(X_1+X_2+\cdots+X_n\right)=\frac{1}{n} \sum_{i=1}^n X_i$	样本均值的期望等于总体均值；样本均值的方差等于总体的方差除以样本个数
样本方差	$S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2=\frac{1}{n-1}\left(\sum_{i=1}^n X_i^2-n \bar{X}^2\right)$	样本方差的期望等于总体的方差
样本标准差	$S=\sqrt{\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2}$
样本 $k$ 阶原点矩	$A_k=\frac{1}{n} \sum_{i=1}^n X_i^k,(k=1,2, \cdots)$
样本 $k$ 阶中心矩	$B_k=\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^k,(k=2,3, \cdots)$

常见的来自正态总体的统计量的分布：

• $\chi^2$ 分布：设 $X_1, X_2, \cdots, X_n$ 相互独立且均来自总体 $X \sim N(0,1)$，则称统计量

$\chi^2=X_1^2+X_2^2+\cdots+X_n^2$

服从自由度为 $n$ 的 $\chi^2$ 分布，记为 $\chi^2 \sim \chi^2(n)$

• $t$ 分布：设 $X \sim N(0,1)$，$Y \sim \chi^2(n)$， 且 $X, Y$ 相互独立,，则称统计量

$T=\frac{X}{\sqrt{Y / n}}$

服从自由度为 $n$ 的 $t$ 分布，记为 $t \sim t(n)$

• $F$ 分布：设 $U \sim \chi^2\left(n_1\right)$，$V \sim \chi^2\left(n_2\right)$，且 $U$，$V$ 相互独立，则称统计量

$F=\frac{U / n_1}{V / n_2}$

服从自由度为 $(n_1,n_2)$ 的 $F$ 分布，记为 $F \sim F\left(n_1, n_2\right)$

正态分布常用结论

设 $X_1, X_2, \cdots, X_n$ 是来自正态总体 $X \sim N\left(\mu, \sigma^2\right)$ 的样本， $\bar{X}$ 是样本均值，$S^2$ 是样本方差,

1. $\bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right)$
2. $\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1)$
3. $\frac{(n-1) S^2}{\sigma^2} \sim \chi^2(n-1)$
4. $\frac{\bar{X}-\mu}{S / \sqrt{n}} \sim t(n-1)$
5. $\bar{X}$ 和 $S^2$ 相互独立

参数估计

点估计

点估计：设总体 $X$ 的分布函数 $F(x ; \theta)$ 的形式已知，$\theta$ 是待估参数，$X_1, X_2, \cdots, X_n$ 是 $X$ 的一个样本，$x_1, x_2, \cdots, x_n$ 是相应的一个样本值点估计问题就是要构造一个适当的统计量 $\hat{\theta}\left(X_1, X_2, \cdots, X_n\right)$，用它的观察值 $\hat{\theta}\left(x_1, x_2, \cdots, x_n\right)$ 作为未知参数 $\theta$ 的近似值。

• $\hat{\theta}\left(X_1, X_2, \cdots, X_n\right)$ 为 $\theta$ 的估计量
• $\hat{\theta}\left(x_1, x_2, \cdots, x_n\right)$ 为 $\theta$ 的估计值

矩估计：用样本矩估计总体矩。

最大似然估计

一次试验的结果 $A$ 发生了，有理由相信 $A$ 发生的概率最大。求解参数取何值时，样本出现的概率最大，用该值作为参数的估计值。

离散型总体未知参数的最大似然估计

离散型总体 $X$ 的分布律 $P\{X=x\}=p(x, \theta)$，$\theta \in \Theta$，其中 $\Theta$ 为未知参数，设 $x_1, x_2, \cdots, x_n$ 是一组样本观测值，求 $\theta$ 的最大似然估计值：

1. 计算似然函数

$L(\theta)=\prod_{i=1}^n p\left(x_i, \theta\right)$

2. 取对数

$\ln L(\theta)=\sum_{i=1}^n \ln p\left(x_i, \theta\right)$

3. 对 $\theta$ 进行求导，并令 $\frac{d}{d \theta} \ln L(\theta)=0$，解出最大似然估计值 $\hat{\theta}$

连续型总体未知参数的极大似然估计

连续型总体 $X$ 的概率密度 $f(x, \theta)$，$\theta \in \Theta$，其中 $\Theta$ 为未知参数，设 $x_1, x_2, \cdots, x_n$ 是一组样本观测值，求 $\theta$ 的最大似然估计值：

1. 计算似然函数

$L(\theta)=\prod_{i=1}^n f\left(x_i, \theta\right)$

2. 取对数

$\ln L(\theta)=\sum_{i=1}^n \ln f\left(x_i, \theta\right)$

3. 对 $\theta$ 进行求导，并令 $\frac{d}{d \theta} \ln L(\theta)=0$，解出最大似然估计值 $\hat{\theta}$

无偏估计

若未知参数 $\theta$ 的估计量 $\hat{\theta}$ 期望值 $E(\hat{\theta})=\theta$，则称 $\hat{\theta}$ 为 $\theta$ 的无偏估计量。

区间估计

双侧区间估计：设总体 $X$ 的分布函数是 $F(x, \theta)$，其中 $\theta$ 是未知参数。对于给定 $\alpha(0<\alpha<1)$，若有样本 $X_1, X_2, \cdots X_n$ 确定的两个统计量 $\underline{\theta}\left(X_1, X_2, \cdots X_n\right)$ 和 $\bar{\theta}\left(X_1, X_2, \cdots X_n\right)$ 满足 $P\{\theta<\theta<\bar{\theta}\} \geq 1-\alpha$，则称随机区间 $(\theta, \bar{\theta})$ 是参数 $\theta$ 的置信度为 $1-\alpha$ 的置信区间, 其中 $\underline{\theta}$ 称为置信下限，$\bar{\theta}$ 称为置信上限，$1-\alpha$ 称为置信度或置信水平

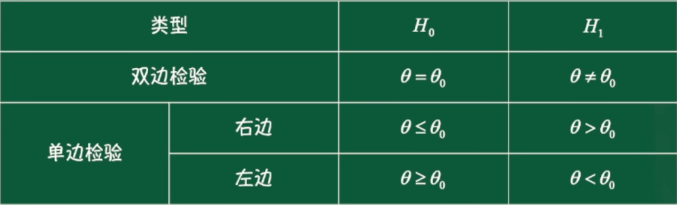
假设检验

原假设：关于总体的假设。

备择假设：与原假设相对立的假设。

检验统计量：检验中用到的统计量。

拒绝域：检验统计量把样本空间分成两个区域，使 $H_0$ 被拒绝的样本观察值所组成的区域为拒绝域。

显著水平：检验统计量落入拒绝域的概率是给定的小概率 $\alpha$。