向量组的线性相关性

向量的线性表示

$n$ 维向量：$n$ 个有次序的数 $a_1,a_2,\cdots,a_n$ 所组成的数组，记作

$\alpha=\left(a_1, a_2, \cdots, a_n\right)$

或

$\alpha=\left(\begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_n \end{array}\right)$

前者行向量，后者为列向量

$a_i$ 称为向量 $\alpha$ 的第 $i$ 个分量。

向量组：若干个维数相同的向量构成一个向量组。

向量的线性组合：设 $A=\left\{\alpha_1, \alpha_2, \cdots, \alpha_m\right\}$ 是一个向量组，$k_1, k_2, \ldots, k_m$ 是 组合系数，则称

$k_1 \alpha_1+k_2 \alpha_2+\cdots+k_m \alpha_m$

是向量 $A$ 的一个线性组合。

向量的线性表示：向量 $\beta$ 能由向量组 $A=\left\{\alpha_1, \alpha_2, \cdots, \alpha_m\right\}$ 线性表示

$\beta=k_1 \alpha_1+k_2 \alpha_2+\cdots+k_m \alpha_m$

【命题】列向量 $b=\left(\begin{array}{c}b_1 \\ b_2 \\ \vdots \\ b_n\end{array}\right)$ 能由矩阵 $A=\left(\begin{array}{cccc}a_{11} & a_{12} & \cdots & a_{1 m} \\ a_{21} & a_{22} & \cdots & a_{2 m} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n m}\end{array}\right)$ 的列向量组线性表示的充分必要条件是下列线性方程：

$x_1\left(\begin{array}{c} a_{11} \\ a_{21} \\ \vdots \\ a_{n 1} \end{array}\right)+x_2\left(\begin{array}{c} a_{12} \\ a_{22} \\ \vdots \\ a_{n 2} \end{array}\right)+\cdots+x_m\left(\begin{array}{c} a_{1 m} \\ a_{2 m} \\ \vdots \\ a_{n m} \end{array}\right)=\left(\begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_n \end{array}\right)$

即 $A x=b$ 有解。

【定理1】 列向量 $b$ 能由矩阵 $A$ 的列向量组 $\left\{a_1, a_2, \cdots, a_m\right\}$ 线性表示的充分必要条件是矩阵 $A=\left(a_1, a_2, \cdots, a_m\right)$ 的秩等于增广矩阵 $B=\left(a_1, a_2, \ldots, a_m, b\right)$ 的秩。

向量组的线性表示

向量组的线性表示：向量组 $B=\left\{\beta_1, \beta_2, \cdots, \beta_l\right\}$ 中的每一个向量 $\beta_i$ 能由向量组 $A=\left\{\alpha_1, \alpha_2, \cdots, \alpha_m\right\}$ 线性表示。

$\beta_i=k_{i 1} \alpha_1+k_{i 2} \alpha_2+\cdots+k_{i m} \alpha_m$

等价向量组：向量组 $B$ 和向量组 $A$ 能相互线性表示，则称两个向量组等价。

【命题】矩阵 $B=\left(\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1 l} \\ b_{21} & b_{22} & \cdots & b_{2 l} \\ \vdots & \vdots & & \vdots \\ b_{n 1} & b_{n 2} & \cdots & b_{n l} \end{array}\right)=\left\{\beta_1, \beta_2, \cdots, \beta_l\right\}$ 的列向量组能由矩阵 $A=\left(\begin{array}{cccc}a_{11} & a_{12} & \cdots & a_{1 m} \\ a_{21} & a_{22} & \cdots & a_{2 m} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n m}\end{array}\right)=\left\{\alpha_1, \alpha_2, \cdots, \alpha_m\right\}$ 的列向量组线性表示的充分必要条件是下列矩阵方程：

$\left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 m} \\ a_{21} & a_{22} & \cdots & a_{2 m} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n m} \end{array}\right)\left(\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 l} \\ x_{21} & x_{22} & \cdots & x_{2 l} \\ \vdots & \vdots & & \vdots \\ x_{m 1} & x_{m 2} & \cdots & x_{m l} \end{array}\right)=\left(\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1 l} \\ b_{21} & b_{22} & \cdots & b_{2 l} \\ \vdots & \vdots & & \vdots \\ b_{n 1} & b_{n 2} & \cdots & b_{n l} \end{array}\right)$

即 $A X=B$ 有解。

讨论 ${(AX)}^T=X^TA^T=B^T$ ，即 $XA=B$

【命题】矩阵 $B=\left(\begin{array}{cccc} b_{11} & b_{21} & \cdots & b_{n 1} \\ b_{12} & b_{22} & \cdots & b_{n 2} \\ \vdots & \vdots & & \vdots \\ b_{1 l} & b_{2 l} & \cdots & b_{n l} \end{array}\right)=\left(\begin{array}{l} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_l \end{array}\right)$ 的行向量组能由矩阵 $A=\left(\begin{array}{cccc}a_{11} & a_{21} & \cdots & a_{n 1} \\ a_{12} & a_{22} & \cdots & a_{n 2} \\ \vdots & \vdots & & \vdots \\ a_{1 m} & a_{2 m} & \cdots & a_{n m}\end{array}\right)=\left(\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_m \end{array}\right)$ 的行向量组线性表示的充分必要条件是下列矩阵方程：

$\left(\begin{array}{cccc} x_{11} & x_{21} & \cdots & x_{m l} \\ x_{12} & x_{22} & \cdots & x_{m 2} \\ \vdots & \vdots & & \vdots \\ x_{1 l} & x_{2 l} & \cdots & x_{m l} \end{array}\right)\left(\begin{array}{cccc} a_{11} & a_{21} & \cdots & a_{n 1} \\ a_{12} & a_{22} & \cdots & a_{n 2} \\ \vdots & \vdots & & \vdots \\ a_{1 m} & a_{2 m} & \cdots & a_{n m} \end{array}\right)=\left(\begin{array}{cccc} b_{11} & b_{21} & \cdots & b_{n 1} \\ b_{12} & b_{22} & \cdots & b_{n 2} \\ \vdots & \vdots & & \vdots \\ b_{1 l} & b_{2 l} & \cdots & b_{n l} \end{array}\right)$

即 $XA=B$ 有解

【定理2】 矩阵 $B$ 的列向量组 $\left\{b_1, b_2, \cdots, b_l\right\}$ 能由矩阵 $A$ 的列向量组 $\left\{a_1, a_2, \cdots, a_m\right\}$ 线性表示的充分必要条件是矩阵 $A=\left(a_1, a_2, \cdots, a_m\right)$ 的秩等于增广矩阵 $(A,B)=\left(a_1, a_2, \ldots, a_m, b_1, b_2, \cdots, b_l\right)$ 的秩。

设矩阵 $A$ 经过一次初等行变换变成矩阵 $B$ ，则 $B$ 的行向量组能由 $A$ 的行向量组线性表示。初等行变换是可逆的，$B$ 也可以经过一次初等变换变回 $A$，因此 $A$ 的行向量组能由 $B$ 的行向量组线性表示。因此若 $A$ 经过一次初等行变换变成矩阵 $B$ ，则 $B$ 的行向量组与 $A$ 的行向量组等价。

【命题】若矩阵 $A$ 与 矩阵 $B$ 行等价，则 $A$ 的行向量组与 $B$ 的行向量组等价。

【命题】若矩阵 $A$ 与 矩阵 $B$ 列等价，则 $A$ 的列向量组与 $B$ 的行向量组等价。

向量组的线性相关性

向量组的线性相关和线性无关：设有向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$，如果存在不全为零的数 $k_1, k_2, \ldots, k_m$，使得

$k_1 a_1+k_2 a_2+\cdots+k_m a_m=0$

则称向量组 $A$ 是线性相关的，否则称该向量组 $A$ 线性无关。

只有一个向量 $a$ 的向量组 $A=\left\{a\right\}$ 线性相关的充分必要条件是 $a$ 是零向量。

【定理3】向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$（$m \geq 2$）线性相关的充分必要条件是向量组中至少一个向量能由其余 $m-1$ 个向量线性表示。

证明：

设向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$（$m \geq 2$）线性相关，则存在不全为零的数 $k_1, k_2, \cdots, k_m$ ，使得

$k_1 a_1+k_2 a_2+\cdots+k_m a_m=0$

不妨设 $k_r \not = 0$，则

$\begin{aligned} & k_r a_r=-\left(k_1 a_1+\cdots+k_{r-1} a_{r-1}+k_{r+1} a_{r+1}+\cdots+k_m a_m\right) \\ & a_r=-\frac{1}{k_r}\left(k_1 a_1+\cdots+k_{r-1} a_{r-1}+k_{r+1} a_{r+1}+\cdots+k_m a_m\right) \end{aligned}$

即 $a_r$ 能由其余 $m-1$ 个向量线性表示。

设有一个向量如 $a_r$ 能由其余 $m-1$ 个向量线性表示

$a_r=k_1 a_1+\ldots+k_{r-1} a_{r-1}+k_{r+1} a_{r+1}+\ldots+k_m a_m$

则存不全为零的数 $k_1, \cdots, k_{r-1},-1, k_{r+1}, \cdots, k_m$ 使得

$k_1 a_1+\ldots+k_{r-1} a_{r-1}+(-1) a_r+k_{r+1} a_{r+1}+\ldots+k_m a_m=0$

即向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$（$m \geq 2$）线性相关。

推论：任何含有零向量的向量组一定线性相关，因此零向量可以由其余线性表示。

推论：向量组线性无关的充分必要条件是组内任何向量都不能由其余向量线性表示。

【定理4_1】设有 $n$ 维列向量组 $\left\{a_1, a_2, \cdots, a_m\right\}$，$A$ 是向量组所构成的 $n \times m$ 矩阵：$A=\left(a_1, a_2, \ldots, a_m\right)$，则以下条件等价：

1. 向量组线性相关
2. 齐次线性方程组 $Ax=0$ 有非零解
3. 矩阵 $A$ 的秩小于向量的个数 $m$：$R(A)<m$

【定理4_2】设有 $n$ 维列向量组 $\left\{a_1, a_2, \cdots, a_m\right\}$，$A$ 是向量组所构成的 $n \times m$ 矩阵：$A=\left(a_1, a_2, \ldots, a_m\right)$，则以下条件等价：

1. 向量组线性无关
2. 齐次线性方程组 $Ax=0$ 只有零解
3. 矩阵 $A$ 的秩等于向量的个数 $m$：$R(A)=m$

一般地，$n$ 维单位向量组：

$\begin{aligned} & e_1=(1,0,0, \cdots, 0) \\ & e_2=(0,1,0, \cdots, 0) \\ & \cdots \cdots \cdots \\ & e_n=(0,0, \cdots, 0,1) \end{aligned}$

线性无关，且任何 $n$ 维向量 $A=(x_1,x_2,\cdots,x_n)$ 都可以用这组向量线性表示

$a=\left(x_1, x_2, \cdots, x_n\right)=x_1 e_1+x_2 e_2+\cdots+x_n e_n$

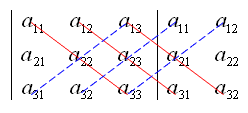
【命题】$n$ 个 $n$ 维向量

$\begin{aligned} & a_1=\left(a_{11}, a_{12}, \cdots, a_{1 n}\right) \\ & a_2=\left(a_{21}, a_{22}, \cdots, a_{2 n}\right) \\ & \cdots \cdots \cdots \\ & a_n=\left(a_{n 1}, a_{n 2}, \cdots, a_{n n}\right) \end{aligned}$

线性相关的充分必要条件是：

$\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right|=0$

【命题】$n$ 个 $n$ 维向量

$\begin{aligned} & a_1=\left(a_{11}, a_{12}, \cdots, a_{1 n}\right) \\ & a_2=\left(a_{21}, a_{22}, \cdots, a_{2 n}\right) \\ & \cdots \cdots \cdots \\ & a_n=\left(a_{n 1}, a_{n 2}, \cdots, a_{n n}\right) \end{aligned}$

线性无关的充分必要条件是：

$\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right| \not =0$

线性相关和线性无关的性质

【定理5】若 $A=\left\{a_1, a_2, \cdots, a_m\right\}$ 线性相关，则向量组 $B=\left\{a_1, a_2, \cdots, a_m,b\right\}$ 也线性相关，反之，若向量组 $B$ 线性无关，则向量组 $A$ 也线性无关。

证明：

若向量组 $A$ 线性相关，则其中至少有一个向量能由其余 $m-1$ 个向量线性表示；

加入向量 $b$ 后，该向量仍然能由其余 $m-1$ 个向量线性表示。

• 相关组扩大后仍然相关
• 无关组缩小后仍然无关

【定理6】若向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$ 线性无关，而向量组 $B=\left\{a_1, a_2, \cdots, a_m,b\right\}$ 线性相关，则向量 $b$ 能由向量组 $A$ 线性表示，且表示是唯一的。

证明：

向量组 $B=\left\{a_1, a_2, \cdots, a_m,b\right\}$ 线性相关

$\Rightarrow$，存在不全为零的数 $k_1, k_2, \ldots, k_m, k_{m+1}$，使得

$k_1 a_1+k_2 a_2+\cdots+k_m a_m+k_{m+1} b=0$

假设 $k_{m+1}=0$，则存在不全为零的数 $k_1, k_2, \ldots, k_m$，使得

$k_1 a_1+k_2 a_2+\cdots+k_m a_m=0$

与向量组 $A$ 线性无关相矛盾，故 $k_{m+1} \not = 0$

于是向量 $b$ 能由向量组 $A$ 线性表示：

$b=-\frac{1}{k_{m+1}}\left(k_1 a_1+k_2 a_2+\cdots+k_m a_m\right)$

假设 $b=p_1 a_1+\cdots+p_m a_m=l_1 a_1+\cdots+l_m a_m$

$\Leftrightarrow$ $\left(p_1-l_1\right) a_1+\cdots+\left(p_m-l_m\right) a_m=0$

又向量组 $A$ 线性无关，有

$p_1-l_1=0, \cdots, p_m-l_m=0$

即

$p_1=l_1, \cdots, p_m=l_m$

所以表示是唯一的。

无关组增加成员变成相关组，该成员能被无关组唯一线性表示。

推论：若向量 $b$ 能由向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$ 线性表示，且表达式不唯一，则 $A$ 必定是线性相关组。

基于定理和推论，可以得到

• 无关组表示向量的形式必唯一；
• 相关组表示向量的形式不唯一。

【定理7】设 $m>n$，则 $m$ 个 $n$ 维向量一定线性相关。

证明：

设有 $m$ 个 $n$ 维向量

$a_1=\left(\begin{array}{l} a_{11} \\ \vdots \\ a_{n 1} \end{array}\right), \cdots, a_m=\left(\begin{array}{l} a_{1 m} \\ \vdots \\ a_{n m} \end{array}\right)(m>n)$

此时

$A=\left(\begin{array}{ccc} a_{11} & \cdots & a_{1 m} \\ \vdots & & \vdots \\ a_{n 1} & \cdots & a_{n m} \end{array}\right)$

又 $R(A) \leq n<m$

齐次线性方程组 $Ax=0$ 有非零解，根据【定理4_1】知向量组线性相关。

【定理8】设 $n$ 维向量组$A=\left\{a_1, a_2, \cdots, a_m\right\}$，$a_1=\left(\begin{array}{c}a_{11} \\ \vdots \\ a_{n 1}\end{array}\right), \cdots, a_m=\left(\begin{array}{c}a_{1 m} \\ \vdots \\ a_{n m}\end{array}\right)$ 线性无关，则 $n+l$ 维向量组 $b_1=\left(\begin{array}{l}a_{11} \\ \vdots \\ a_{n 1} \\ b_{11} \\ \vdots \\ b_{l 1}\end{array}\right), \cdots, b_m=\left(\begin{array}{l}a_{1 m} \\ \vdots \\ a_{n m} \\ b_{1 m} \\ \vdots \\ b_{l m}\end{array}\right)$ 也线性无关。

证明：

因为向量组 $A$ 线性无关，根据【定理4_2】知 $R(A)=R\left(a_1, \cdots, a_m\right)=m$

因为 $R\left(b_1, \cdots, b_m\right) \geq R\left(a_1, \cdots, a_m\right)=m$，又 $R\left(b_1, \ldots, b_m\right) \leq m$

所以 $R\left(b_1, \ldots, b_m\right)=m$，根据【定理4_2】知向量组 $\left\{b_1, \cdots, b_m\right\}$ 线性无关。

无关组加长后仍然无关

向量组的秩与极大无关组

向量组的极大无关组：设有向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$ 的一个部分组 $B=\left\{a_1, a_2, \cdots, a_r\right\}$ 满足条件：

1. 向量组 $B$ 线性无关
2. 再增加向量组 $A$ 中的一个向量 $a$ 的向量组 $\left\{a_1, a_2, \cdots, a_r, a\right\}$ 后总是线性相关

则称向量组 $B$ 是向量组 $A$ 的一个极大线性无关组/极大无关组/最大无关组。

【命题】向量组 $A$ 的极大无关组 $B$ 与全组等价。

向量组 $A$ 的极大无关组一般不是唯一的，但由【命题】知以及等价关系的传递性：

向量组的任意两个极大无关组等价。

【定理9】设向量组 $B=\left\{b_1, b_2, \cdots, b_l\right\}$ 能由向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$ 线性表示，若 $l>m$ ，则向量组 $B$ 一定线性相关。

证明：

向量组 $B=\left\{b_1, b_2, \cdots, b_l\right\}$ 能由向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$ 线性表示

$\left\{\begin{array}{l} b_1=c_{11} a_1+\ldots+c_{m 1} a_m \\ \cdots \cdots \cdots \cdots \cdots \cdots\\ b_l=c_{1 l} a_1+\ldots+c_{m l} a_m \end{array}\right.$

或

$\left(b_1, \cdots, b_l\right)=\left(a_1, \cdots, a_m\right)\left(\begin{array}{ccc} c_{11} & \cdots & c_{1 l} \\ \vdots & \cdots & \vdots \\ c_{m 1} & \cdots & c_{m l} \end{array}\right)$

讨论方程

$\left(\begin{array}{ccc} c_{11} & \cdots & c_{1 l} \\ \vdots & \cdots & \vdots \\ c_{m l} & \cdots & c_{m l} \end{array}\right)\left(\begin{array}{c} x_1 \\ \vdots \\ x_l \end{array}\right)=\left(\begin{array}{c} 0 \\ \vdots \\ 0 \end{array}\right)$

因为 $R(C) \leq m < l$

其次线性方程组有非零解 $\left(k_1, \ldots, k_l\right) \neq(0, \ldots, 0)$

$\begin{array}{r}k_1 b_1+\cdots+k_l b_l =\left(b_1, \cdots, b_l\right)\end{array}\left(\begin{array}{c}k_1 \\ \vdots \\ k_l\end{array}\right)=\left(a_1, \cdots, a_m\right) C\left(\begin{array}{c}k_1 \\ \vdots \\ k_l\end{array}\right)=\left(a_1, \ldots, a_m\right)\left(\begin{array}{c} 0 \\ \vdots \\ 0 \end{array}\right)$

推论：无关组不能由更少的向量线性表示。

推论：两个等价的无关组所含向量的个数相同。

【命题】向量组 $A$ 的任意两个极大无关组等价，且含有相同个数的向量。

向量组的秩：向量组 $A$ 的极大无关组中所含向量的个数称为向量组的秩，记作 $R_A$。

一个 $n \times m$ 矩阵 $A$ 的 $n$ 行构成行向量组 ，$A$ 的 $m$ 列构成列向量组.

下面来讨论矩阵 $A$ 的秩，$A$ 的行向量组秩与列向量组秩的关系。

【引理】设矩阵 $A$ 有一个 $k$ 阶子式 $D \neq 0$，则：

1. $D$ 所在的 $k$ 列的列向量组线性无关
2. $D$ 所在的 $k$ 行的行向量组线性无关

证明：

设 $n \times m$ 矩阵 $A$ 有一个$k$ 阶子式 $D \neq 0$，即

$D=\left|\begin{array}{ccc} a_{i_1 j_1} & \cdots & a_{i_1 j_k} \\ \vdots & & \vdots \\ a_{i_k j_1} & \cdots & a_{i_k j_k} \end{array}\right| \neq 0$

$D$ 所在的 $k$ 列的列向量构成的矩阵 $D_{\text {column}}$

$D_{\text {column}}=\left(\begin{array}{ccc} a_{1 j_1} & \cdots & a_{1 j_k} \\ \vdots & & \vdots \\ a_{n j_1} & \cdots & a_{n j_k} \end{array}\right)$

有一个 $k$ 阶子式 $D \neq 0$，故 $R(D_{\text {column}})=k$，由【定理4_2】知 $D_{\text {column}}$ 的列向量组线性无关。

$D$ 所在的 $k$ 行的行向量构成的矩阵 $D_{\text {row}}$

$D_{\text {row}}=\left(\begin{array}{ccc} a_{i_1 1} & \cdots & a_{i_1 n} \\ \vdots & & \vdots \\ a_{i_k 1} & \cdots & a_{n n} \end{array}\right)$

有一个 $k$ 阶子式 $D \neq 0$，故 $R(D_{\text {row}})=k$，由【定理4_2】知 $D_{\text {row}}$ 的行向量组线性无关。

【定理10】一个矩阵的秩等于它的列向量组的秩，也等于它的行向量组的秩。

证明：

设矩阵 $A$ 的秩 $R(A)=r$，则 $A$ 有一个 $r$ 阶子式 $D \not = 0$，

由前面的引理，

• $D$ 所在的 $r$ 列的列向量线性无关，所以 $A$ 的列向量组的秩 $R_{A_\text {column}} \geq r=R(A)$ 。
• $D$ 所在的 $r$ 行的行向量线性无关，所以 $A$ 的行向量组的秩 $R_{A_{\text {row}}} \geq r=R(A)$ 。

又 $R_A=r=R(A)$

若不然，则 $R_A=r^{\prime}>r=R(A)$，则 $A$ 的列（行）向量组有 $r^{\prime}$ 个向量线性无关。

由【定理4_2】知由这 $r$ 列（行）向量组成矩阵 $A^{\prime}$ 的秩 $R(A^{\prime})=r^{\prime}$

得 $R(A^{\prime})=r^{\prime}>r=R(A)$，矛盾

所以 $R_A=r=R(A)$

• 矩阵 $A$ 的秩等于其列向量组的秩
• 矩阵 $A$ 的秩等于其行向量组的秩

矩阵的秩=行秩=列秩

求解向量组的秩与极大无关组的方法

1. 以列向量组 $A=\left\{a_1, a_2, \cdots, a_m\right\}$ 构造矩阵 $A$
2. 用初等行变换将矩阵 $A$ 化为行阶梯形矩阵 $B$

$R_A=R(A)=R(B)=r$

$B$ 的各行非零首元所在列构成 $B$ 列向量组的极大无关组中的其中一个（【引理】）

$\Rightarrow$ $A$ 的对应列构成 $A$ 列向量组的极大无关组

3. 用初等行变换将行阶梯形矩阵 $B$ 化为行最简形矩阵 $C$

关系同上

齐次线性方程组的解的结构

$n$ 元齐次线性方程组

$\left\{\begin{array}{c} a_{11} x_1+a_{12} x_2+\cdots+a_{1 n} x_n=0 \\ a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n=0 \\ \cdots \cdots \cdots \cdots \\ a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n=0 \end{array}\right.$

即 $Ax=0$

若 $x=\xi_1=\left(\xi_{11}, \xi_{21}, \ldots, \xi_{n 1}\right)^T$ 满足 $Ax=0$，则称 $x$ 为解向量

• 若 $x=\xi_1$，$x=\xi_2$ 是 $Ax=0$ 的解，则 $x=\xi_1+\xi_2$ 也是 $Ax=0$ 的解
• 若 $x=\xi_1$ 是 $Ax=0$ 的解，则 $x=k\xi_1$ 也是 $Ax=0$ 的解

推广：若 $x=\xi_1,, \cdots, x=\xi_l$ 是 $Ax=0$ 的解，则 $x=k_1 \xi_1+\cdots+k_l \xi_l$ 也是 $Ax=0$ 的解

解集：全体解向量 $x$ 组成的集合 $S$。

$S=\{x \mid A x=0\}$

以上性质表明，齐次线性方程组的解集关于线性运算是封闭的。

$n$ 元齐次线性方程组 $Ax=0$ 必有零解

• 若 $R(A)=r=n$，方程组只有零解，$S={x|x=0}$
• 若 $R(A)=r<n$，方程组有无穷多解

找到解集 $S$ 中的 $l$ 个线性无关的解 $\xi_1, \cdots, \xi_l$，使得 $S$ 中的任一解都可由该组解线性表示（通解）

$x=k_1 \xi_1+\ldots+k_l \xi_l$

则 $n$ 元齐次线性方程组 $Ax=0$ 的解集表示为：

$S=\left\{k_1 \xi_1+\cdots+k_l \xi_l \mid k_1, \cdots, k_l \text { 是任意实数 }\right\}$

基础解系：$n$ 元齐次线性方程组 $Ax=0$ 的解集 $S$ 的一个极大无关组。

【定理11】设 $A$ 是一个 $m \times n$ 的矩阵，若 $R(A)=r<n$，则 $n$ 元齐次线性方程组 $Ax=0$ 有基础解系：

$\xi_1, \xi_2, \cdots, \xi_{n-r}$

满足：

1. 基础解系线性无关
2. 任一解都能由基础解系线性表示

证明：

$R(A)=r<n$

经过若干次初等行变换，将 $A$ 化成行最简形 $B$

$A \rightarrow \cdots \rightarrow\left(\begin{array}{cccccc} 1 & \cdots & 0 & b_{11} & \cdots & b_{1, n-r} \\ \vdots & & \vdots & \vdots & & \vdots \\ 0 & \cdots & 1 & b_{r 1} & \cdots & b_{r, n-r} \\ 0 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & 0 \end{array}\right)=B$

假定前 $r$ 个是非自由未知数，后 $n-r$ 个是自由未知数

对应的 $n$ 元齐次线性方程组：

$\left\{\begin{array}{c} x_1+b_{11} x_{r+1}+\cdots+b_{1, n-r} x_n=0 \\ x_2+b_{21} x_{r+1}+\cdots+b_{2, n-r} x_n=0 \\ \cdots \cdots \cdots \cdots \cdots \\ x_r+b_{r 1} x_{r+1}+\cdots+b_{r, n-r} x_n=0 \end{array}\right.$

$\left\{\begin{array}{c} x_1=-b_{11} x_{r+1}-\cdots-b_{1, n-r} x_n \\ x_2=-b_{21} x_{r+1}-\cdots-b_{2, n-r} x_n \\ \cdots \cdots \cdots \cdots \cdots \\ x_r=-b_{r 1} x_{r+1}-\cdots-b_{r, n} x_n \end{array}\right.$

$x_1, \cdots, x_r$ 是非自由未知数，$x_{r+1}, \cdots, x_n$ 是自由未知数

令自由未知数依次为：

$\left(\begin{array}{c} x_{r+1} \\ x_{r+2} \\ \vdots \\ x_n \end{array}\right)=\left(\begin{array}{c} 1 \\ 0 \\ \vdots \\ 0 \end{array}\right)\left(\begin{array}{c} 0 \\ 1 \\ \vdots \\ 0 \end{array}\right)\cdots\left(\begin{array}{c} 0 \\ 0 \\ \vdots \\ 1 \end{array}\right)$

得到 $n-r$ 个解向量：

$\xi_1=\left(\begin{array}{c} -b_{11} \\ -b_{21} \\ \vdots \\ -b_{r 1} \\ 1 \\ 0 \\ \vdots \\ 0 \end{array}\right), \xi_2=\left(\begin{array}{c} -b_{12} \\ -b_{22} \\ \vdots \\ -b_{r 2} \\ 0 \\ 1 \\ \vdots \\ 0 \end{array}\right) \cdots \xi_{n-r}=\left(\begin{array}{c} -b_{1, n-r} \\ -b_{2, n-r} \\ \vdots \\ -b_{r, n-r} \\ 0 \\ 0 \\ \vdots \\ 1 \end{array}\right)$

由【定理8】知自由未知数向量组线性无关，加长后的解向量组也线性无关。

下面说明这组解向量能线性表示 $n$ 元齐次线性方程组的任一解。

设 $x$ 是 $Ax=0$ 的任一解，则：

$x=\left(\begin{array}{c} -b_{11} x_{r+1}-b_{12} x_{r+2}-\cdots-b_{1, n-r} x_n \\ -b_{21} x_{r+1}-b_{22} x_{r+2}-\cdots-b_{2, n-r} x_n \\ \vdots \\ -b_{r 1} x_{r+1}-b_{r 2} x_{r+2}-\cdots-b_{r, n-r} x_n \\ x_{r+1} \\ x_{r+2} \\ \vdots \\ x_n \end{array}\right)=\left(\begin{array}{c} -b_{11} x_{r+1} \\ -b_{21} x_{r+1} \\ \vdots \\ -b_{r 1} x_{r+1} \\ x_{r+1} \\ 0 \\ \vdots \\ 0 \end{array}\right)+\left(\begin{array}{c} -b_{12} x_{r+2} \\ -b_{22} x_{r+2} \\ \vdots \\ -b_{r 2} x_{r+2} \\ 0 \\ x_{r+2} \\ \vdots \\ 0 \end{array}\right)+\cdots+\left(\begin{array}{c} -b_{1, n-r} x_n \\ -b_{2, n-r} x_n \\ \vdots \\ -b_{r, n-r} x_n \\ 0 \\ 0 \\ \vdots \\ x_n \end{array}\right)$

$x=x_{r+1}\left(\begin{array}{c} -b_{11} \\ -b_{21} \\ \vdots \\ -b_{r 1} \\ 1 \\ 0 \\ \vdots \\ 0 \end{array}\right)+x_{r+2}\left(\begin{array}{l} -b_{12} \\ -b_{22} \\ \vdots \\ -b_{r 2} \\ 0 \\ 1 \\ \vdots \\ 0 \end{array}\right)+\cdots+x_n\left(\begin{array}{c} -b_{1, n-r} \\ -b_{2, n-r} \\ \vdots \\ -b_{r, n-r} \\ 0 \\ 0 \\ \vdots \\ 1 \end{array}\right)==x_{r+1} \xi_1+x_{r+2} \xi_2 \ldots+x_{n-r} \xi_{n-r}$

因此这组线性无关的解向量组能线性表示 $n$ 元齐次线性方程组的任一解。

【定理7】设 $A$ 是一个 $m \times n$ 的矩阵，若 $R(A)=r<n$，则 $n$ 元齐次线性方程组 $Ax=0$ 的解集 $S$ 的秩 $R_S=n-r$，即

$R_S+R(A)=n$

非齐次线性方程组的解的结构

$n$ 元非齐次线性方程组

$\left\{\begin{array}{c} a_{11} x_1+a_{12} x_2+\cdots+a_{1 n} x_n=0 \\ a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n=0 \\ \cdots \cdots \cdots \cdots \\ a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n=0 \end{array}\right.$

即 $Ax=b$

对应 $n$ 元齐次线性方程 $Ax=0$

• 若 $x=\eta_1$，$x=\eta_2$ 是 $Ax=b$ 的解，则 $x=\eta_1-\eta_2$ 是 $Ax=0$ 的解
• 若 $x=\eta$ 是 $Ax=b$ 的解，$x=\xi$ 是 $Ax=0$ 的解，则 $x=\xi+\eta$ 是 $Ax=b$ 的解

$n$ 元齐次线性方程组 $Ax=b$

• 若 $R(A)=R(A,b)=r=n$，方程组有唯一解
• 若 $R(A)=R(A,b)=r<n$，方程组有无穷多解

设 $x=\eta^*$ 是非齐次线性方程组 $Ax=b$ 的解

其对应齐次方程组 $Ax=0$ 的通解为：$x=\xi=k_1 \xi_1+\ldots+k_{n-r} \xi_{n-r}$

设 $x=\eta$ 是非齐次线性方程组 $Ax=b$ 的解

则 $\eta-\eta^*$ 是齐次方程组 $Ax=0$ 的解

故

$\eta-\eta^*=k_1 \xi_1+\ldots+k_{n-r} \xi_{n-r}$

非齐次方程组的通解：

$\eta=k_1 \xi_1+\ldots+k_{n-r} \xi_{n-r}+\eta^*$

【命题1】设 $\eta_1, \cdots, \eta_s$ 是非齐次线性方程组 $Ax=b$ 的 $s$ 个解，则 $x=k_1 \eta_1+\cdots+k_s \eta_s$ 也是 $Ax=b$ 的解的充分必要条件是：$k_1+\cdots+k_s=1$。

证明：

$x=k_1 \eta_1+\cdots+k_s \eta_s$ 是 $Ax=b$ 的解 $\Leftarrow k_1+\cdots+k_s=1$。

$\begin{aligned} & A\left(k_1 \eta_1+\cdots+k_s \eta_s\right) \\ = & k_1 A \eta_1+\cdots+k_s A \eta_s\\ = & k_1 b+\cdots+k_s b \\ = & \left(k_1+\cdots+k_s\right) b\\ = & b \end{aligned}$

$x=k_1 \eta_1+\cdots+k_s \eta_s$ 是 $Ax=b$ 的解 $\Rightarrow k_1+\cdots+k_s=1$。

$\begin{aligned} b & =A x\\ & =A\left(k_1 \eta_1+\ldots+k_s \eta_s\right) \\ & =k_1 A \eta_1+\ldots+k_s A \eta_s\\ & =k_1 b+\ldots+k_s b \\ & =\left(k_1+\ldots+k_s\right) b \quad \\ \end{aligned}$

又 $b \neq 0$

故 $k_1+\cdots+k_s=1$

【命题2】设 $\eta_1, \cdots, \eta_s$ 是非齐次线性方程组 $Ax=b$ 的 $s$ 个解，则 $x=k_1 \eta_1+\cdots+k_s \eta_s$ 也是导出组 $Ax=0$ 的解的充分必要条件是：$k_1+\cdots+k_s=0$。

证明：

$x=k_1 \eta_1+\cdots+k_s \eta_s$ 是 $Ax=0$ 的解 $\Leftarrow k_1+\cdots+k_s=0$。

$\begin{aligned} & A\left(k_1 \eta_1+\cdots+k_s \eta_s\right) \\ = & k_1 A \eta_1+\cdots+k_s A \eta_s\\ = & k_1 b+\cdots+k_s b \\ = & \left(k_1+\cdots+k_s\right) b\\ = & 0 \end{aligned}$

$x=k_1 \eta_1+\cdots+k_s \eta_s$ 是 $Ax=0$ 的解 $\Rightarrow k_1+\cdots+k_s=0$。

$\begin{aligned} 0 & =A x\\ &=A\left(k_1 \eta_1+\ldots+k_s \eta_s\right) \\ & =k_1 A \eta_1+\ldots+k_s A \eta_s\\ & =k_1 b+\ldots+k_s b \\ & =\left(k_1+\ldots+k_s\right) b \quad \\ \end{aligned}$

又 $b \neq 0$

故 $k_1+\cdots+k_s=0$

【命题3】设 $\eta_1, \cdots, \eta_s,\eta$ 是非齐次线性方程组 $Ax=b$ 的 $s+1$ 个线性无关的解，则 $\eta_1-\eta, \cdots, \eta_s-\eta$ 是导出组 $Ax=0$ 的 $s$ 个线性无关的解。

证明：

设

$k_1\left(\eta_1-\eta\right)+\cdots+k_s\left(\eta_s-\eta\right)=0$

$k_1 \eta_1+\cdots+k_s \eta_s-\left(k_1+\cdots+k_s\right) \eta=0$

由于 $\eta_1, \cdots, \eta_s,\eta$ 是非齐次线性方程组 $Ax=b$ 的 $s+1$ 个线性无关的解

所以 $k_1=\cdots=k_s=0$

所以 $\eta_1-\eta, \cdots, \eta_s-\eta$ 是导出组 $Ax=0$ 的 $s$ 个线性无关的解。

【命题4】 设 $n$ 元非齐次线性方程组 $Ax=b$ 有无穷多解，且设 $R(A)=R(A,b)=r<n$。设 $\eta^*$ 是非齐次线性方程组 $Ax=b$ 的解，$\xi_1, \cdots, \xi_{n-r}$ 是导出组 $Ax=0$ 的基础解系，则

1. $\eta *, \xi_1, \cdots, \xi_{n-r}$ 线性无关
2. $\eta *, \eta^* +\xi_1, \ldots,\eta^{*} \xi_{n-r}$ 是 $Ax=b$ 的 $n-r+1$ 个线性无关的解

证明：

设

$k \eta^*+k_1 \xi_1+\ldots+k_{n-r} \xi_{n-r}=0$

若 $k \neq 0$，则

$\eta^*=-\frac{1}{k}\left(k_1 \xi_1+\ldots+k_{n-r} \xi_{n-r}\right)$

说明 $\eta^*$ 是齐次线性方程组 $Ax=0$ 的解，矛盾！

所以 $k=0$

$k_1 \xi_1+\cdots+k_{n-r} \xi_{n-r}=0$

又 $\xi_1, \cdots, \xi_{n-r}$ 是导出组 $Ax=0$ 的基础解系线性无关

所以 $k_1=\cdots=k_s=0$

所以 $\eta *, \xi_1, \cdots, \xi_{n-r}$ 线性无关。

由相关性质，$\eta *, \eta^*+\xi_1, \cdots, \eta^{*+} \xi_{n-r}$ 是 $Ax=b$ 的解

设

$k \eta^*+k_1\left(\eta^*+\xi_1\right)+\cdots+k_{n-r}\left(\eta^*+\xi_{n-r}\right)=0$

$\left(k+k_1+\cdots+k_{n-r}\right) \eta^*+k_1 \xi_1+\cdots+k_{n-r} \xi_{n-r}=0$

由1可知 $\eta *, \xi_1, \cdots, \xi_{n-r}$ 线性无关

所以 $k_1=\cdots=k_{n-r}=0=k$

所以 $\eta *, \eta^* +\xi_1, \ldots,\eta^{*} \xi_{n-r}$ 是 $Ax=b$ 的 $n-r+1$ 个线性无关的解

【命题5】 设 $n$ 元非齐次线性方程组 $Ax=b$ 有无穷多解，且设 $R(A)=R(A,b)=r<n$。设 $\eta_1, \cdots, \eta_{n-r+1},\eta$ 是非齐次线性方程组 $Ax=b$ 的 $n-r+1$ 个线性无关的解，则 $Ax=b$ 的任一解 $x$ 均可以表示为 $n-r+1$ 个线性无关的解的加权平均。

证明：

假设 $x, \eta_1, \cdots, \eta_{n-r+1}$ 是非齐次线性方程组 $Ax=b$ 的解

若它们线性无关，由【命题3】

$x-\eta_1, \cdots, x-\eta_{n-r+1}$

是导出组 $Ax=0$ 的 $n-r+1$ 个线性无关的解。

由【定理7】知 $Ax=0$ 的解集的秩为 $n-r$ ，矛盾！

则 $x, \eta_1, \cdots, \eta_{n-r+1}$ 线性相关。

因此 $x$ 可由 $\eta_1, \cdots, \eta_{n-r+1}$ 线性表示

设 $x=k_1 \eta_1+\ldots+k_{n-r+1} \eta_{n-r+1}$

$\begin{aligned} b & =A x\\ & =A\left(k_1 \eta_1+\ldots+k_s \eta_s\right) \\ & =k_1 A \eta_1+\ldots+k_s A \eta_s\\ & =k_1 b+\ldots+k_s b \\ & =\left(k_1+\ldots+k_s\right) b \quad \\ \end{aligned}$

又 $b \neq 0$

故 $k_1+\cdots+k_s=1$

推论： 设 $n$ 元非齐次线性方程组 $Ax=b$ 有无穷多解，且设 $R(A)=R(A,b)=r<n$。设 $\eta_1, \cdots, \eta_{n-r+1},\eta$ 是非齐次线性方程组 $Ax=b$ 的 $n-r+1$ 个线性无关的解，则 $Ax=b$ 的解集为：$S=\left\{k_1 \eta_1+\ldots+k_{n-r+1} \eta_{n-r+1} \mid \sum_{i=1}^{n-r+1} k_i=1, k_i \in \mathbb{R}\right\}$。

向量空间

向量空间：设 $\varnothing \neq V \subseteq \mathbb{R}^n$，若集合 $V$ 对向量线性运算封闭，则称 $V$ 是一个向量空间。

若集合 $V$ 对向量线性运算封闭：$\forall a, b \in V \Rightarrow a+b \in V, \quad \lambda a \in V$

任何向量空间必须含有零向量，若 $a \in V$，则 $0 a=0 \in V$

设有一组 $n$ 维向量 $a_1, \cdots, a_m$ ，一切线性组合的集合记为 $L$：

$L=\left\{\lambda_1 a_1+\ldots+\lambda_m a_m \mid \lambda_1, \ldots, \lambda_m \in \mathbb{R}\right\}$

设 $x=\lambda_1 a_1+\ldots+\lambda_m a_m$，$y=\mu_1 a_1+\ldots+\mu_m a_m$

$\begin{aligned} x+y & =\left(\lambda_1 a_1+\ldots+\lambda_m a_m\right)+\left(\mu_1 a_1+\ldots+\mu_m a_m\right) =\left(\lambda_1+\mu_1\right) a_1+\ldots+\left(\lambda_m+\mu_m\right) a_m \in L \end{aligned}$

$\begin{aligned} k x & =k\left(\lambda_1 a_1+\ldots+\lambda_m a_m\right) =k \lambda_1 a_1+\ldots+k \lambda_m a_m \in L \end{aligned}$

则 $L$ 是一个由前面这组向量生成的向量空间。

设向量组 $a_1, \cdots, a_m$ 可有向量组 $b_1, \ldots, b_l$ 线性表示，则：

$L\left(a_1, \ldots, a_m\right) \subseteq L\left(b_1, \ldots, b_l\right)$

【命题】设向量组 $a_1, \cdots, a_m$ 可有向量组 $b_1, \ldots, b_l$ 等价，则：

$L\left(a_1, \cdots, a_m\right)=L\left(b_1, \cdots, b_l\right)$

等价向量组有相同的向量空间

向量的基和维数：设 $V$ 是一个向量空间，如果 $V$ 中有 $r$ 个向量 $a_1, \cdots, a_r$，满足：

1. $a_1, \cdots, a_r$ 线性无关
2. $V$ 中任一向量都可由 $a_1, \ldots, a_r$ 线性表示（等价于 $V$ 可由向量组生成）

$V=\left\{\lambda_1 a_1+\ldots+\lambda_r a_r \mid \lambda_1, \ldots, \lambda_r \in \mathbb{R}\right\}$

则称 $a_1, \cdots, a_r$ 是 $V$ 的一个基，$r$ 称为 $V$ 的维数，称 $V$ 是 $r$ 维空间。

• 只有零向量的向量空间没有基。

• 向量空间 $V$ 的基就是 $V$ 的一个极大无关组，$V$ 的维数就是极大无关组的向量个数。

• $\mathbb{R}^n$ 中的任何含有非零向量的向量空间都有基。

类比【定理11】，设 $A$ 是一个 $m \times n$ 的矩阵，若 $R(A)=r<n$，则 $n$ 元齐次线性方程组 $Ax=0$ 有基础解系：$\xi_1, \xi_2, \cdots, \xi_{n-r}$ 是解空间 $S$ 的一个基，方程组的 $n-r$ 解空间由这组基生成。

$S=\left\{c_1 \xi_1+\ldots+c_{n-r} \xi_{n-r} \mid c_1, \ldots, c_{n-r} \in \mathbb{R}\right\}$

向量在基中的坐标

过渡矩阵：旧基 $A$，新基 $B$，满足

$B=A P$

则 $P=A^{-1} B$。

旧基下的坐标与新基下的坐标的转换的转换：

设 $x$ 在旧基 $A$ 下的坐标为 $y^T$（$y$ 是列向量）， $x$ 在新基 $B$ 下的坐标为 $z^T$（$z$ 是列向量）

$Ay^T=Bz^T=APz^T$

$z^T=P^{-1}y^T$