行列式

• 二阶与三阶行列式
• 全排列和对换
• 行列式的性质
• 行列式按行（列）展开

二阶与三阶行列式

==解二元线性方程组 $\longrightarrow$ 二阶行列式==

$\left\{\begin{array}{l} a_{11} x_1+a_{12} x_2=b_1, \\ a_{21} x_1+a_{22} x_2=b_2 . \end{array}\right.$

• ${b_1}$ 和 ${b_2}$：常数
• ${a_{ij}}$：第$i$个方程的第 $j$ 个未知数 $x_j$ 的系数

两个方程两端同时乘以 $a_{22}$ 和 $a_{12}$，

$\left\{\begin{array}{l} a_{22}\left(a_{11} x_1+a_{12} x_2\right)=a_{22} b_1 \\ a_{12}\left(a_{21} x_1+a_{22} x_2\right)=a_{12} b_2 \end{array}\right.$

两式相减，

$\left(a_{11} a_{22}-a_{12} a_{21}\right) x_1=b_1 a_{22}-a_{12} b_2$

两个方程两端同时乘以 $a_{21}$ 和 $a_{11}$，

$\left\{\begin{array}{l} a_{21}\left(a_{11} x_1+a_{12} x_2\right)=a_{21} b_1 \\ a_{11}\left(a_{21} x_1+a_{22} x_2\right)=a_{11} b_2 \end{array}\right.$

两式相减，

$\left(a_{11} a_{22}-a_{12} a_{21}\right) x_2=a_{11} b_2-b_1 a_{21}$

如果$a_{11} a_{22}-a_{12} a_{21}\neq0$，可以解出：

$x_1=\frac{b_1 a_{22}-a_{12} b_2}{a_{11} a_{22}-a_{12} a_{21}} \quad x_2=\frac{a_{11} b_2-b_1 a_{21}}{a_{11} a_{22}-a_{12} a_{21}}$

数表：

$\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}$

表达式：$a_{11} a_{22}-a_{12} a_{21}$

二阶行列式：$\left|\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right|$

• $a_{ij}$：$(i,j)$元，位于第 $i$ 行第 $j$ 列的元素
• $i$：行标
• $j$：列标

利用二阶行列式，式子简记为：

$b_1 a_{22}-a_{12} b_2=\left|\begin{array}{ll} b_1 & a_{12} \\ b_2 & a_{22} \end{array}\right|, \quad a_{11} b_2-b_1 a_{21}=\left|\begin{array}{ll} a_{11} & b_1 \\ a_{21} & b_2 \end{array}\right| .$

若记

$D=\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|, \quad D_1=\left|\begin{array}{ll} b_1 & a_{12} \\ b_2 & a_{22} \end{array}\right|, \quad D_2=\left|\begin{array}{ll} a_{11} & b_1 \\ a_{21} & b_2 \end{array}\right|,$

利用二阶行列式的概念，改写 $x_1$，$x_2$ 的表示：

$x_1=\frac{D_1}{D}=\frac{\left|\begin{array}{ll} b_1 & a_{12} \\ b_2 & a_{22} \end{array}\right|}{\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|}, \quad x_2=\frac{D_2}{D}=\frac{\left|\begin{array}{ll} a_{11} & b_1 \\ a_{21} & b_2 \end{array}\right|}{\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|} .$

• $D$：系数行列式

==解三元线性方程组 $\longrightarrow$ 三阶行列式==

$\left\{\begin{array}{l} a_{11} x_1+a_{12} x_2+a_{13} x_3=b_1 \\ a_{21} x_1+a_{22} x_2+a_{23} x_3=b_2 \\ a_{31} x_1+a_{32} x_2+a_{33} x_3=b_3 \end{array}\right.$

• ${b_1}$、${b_2}$ 和 ${b_3}$：常数
• ${a_{ij}}$：第 $i$ 个方程的第 $j$ 个未知数 $x_j$ 的系数

后两个方程两端同时乘以 $a_{33}$ 和 $a_{22}$，

$\left\{\begin{array}{l} a_{33}\left(a_{21} x_1+a_{22} x_2+a_{23} x_3\right)=a_{33} b_2 \\ a_{23}\left(a_{31} x_1+a_{32} x_2+a_{33} x_3\right)=a_{23} b_3 \end{array}\right.$

两式相减，

$\left(a_{21} a_{33}-a_{23} a_{31}\right) x_1+\left(a_{22} a_{33}-a_{23} a_{32}\right) x_2=b_2 a_{33}-a_{23} b_3$

后两个方程两端同时乘以 $a_{32}$ 和 $a_{22}$，

$\left\{\begin{array}{l} a_{32}\left(a_{21} x_1+a_{22} x_2+a_{23} x_3\right)=a_{32} b_2 \\ a_{22}\left(a_{31} x_1+a_{32} x_2+a_{33} x_3\right)=a_{22} b_3 \end{array}\right.$

两式相减，

$\left(a_{21} a_{32}-a_{22} a_{31}\right) x_1+\left(a_{23} a_{32}-a_{22} a_{33}\right) x_3=b_2 a_{32}-a_{22} b_3$

目前得到有方程（1）（2），

$\begin{aligned} \left(a_{21} a_{33}-a_{23} a_{31}\right) x_1+\left(a_{22} a_{33}-a_{23} a_{32}\right) x_2 & =b_2 a_{33}-a_{23} b_3 \\ \left(a_{21} a_{32}-a_{22} a_{31}\right) x_1+\left(a_{23} a_{32}-a_{22} a_{33}\right) x_3 & =b_2 a_{32}-a_{22} b_3 \end{aligned}$

原方程组的第一个方程同时乘以 $a_{22} a_{33}-a_{23} a_{32}$ ，得到方程（3）’

$\begin{aligned} &\left(a_{11} a_{22} a_{33}-a_{11} a_{23} a_{32}\right) x_1+\left(a_{12} a_{22} a_{33}-a_{12} a_{23} a_{32}\right) x_2+\left(a_{13} a_{22} a_{33}-a_{13} a_{23} a_{32}\right) x_3=b_1 a_{22} a_{33}-b_1 a_{23} a_{32} \end{aligned}$

方程（1）两端乘以${-a_{12}}$，得到方程（1）‘

$\begin{aligned} \left(a_{12} a_{23} a_{31}-a_{12} a_{21} a_{33}\right) x_1 &+\left(a_{12} a_{23} a_{32}-a_{12} a_{22} a_{33}\right) x_2=a_{12} a_{23} b_3-a_{12} b_2 a_{33} \end{aligned}$

方程（2）两端乘以${a_{13}}$，得到方程（2）‘

$\begin{aligned} \left(a_{13} a_{21} a_{32}-a_{13} a_{22} a_{31}\right) x_1 &+\left(a_{13} a_{23} a_{32}-a_{13} a_{22} a_{33}\right) x_3 a_{13} b_2 a_{32}-a_{13} a_{22} b_3 \end{aligned}$

联立方程（1）‘、（2）‘、（3）‘

$\begin{aligned} \left(a_{11} a_{22} a_{33}-a_{11} a_{23} a_{32}\right) x_1+\left(a_{12} a_{22} a_{33}-a_{12} a_{23} a_{32}\right) x_2+\left(a_{13} a_{22} a_{33}-a_{13} a_{23} a_{32}\right) x_3 & =b_1 a_{22} a_{33}-b_1 a_{23} a_{32} \\ \left(a_{12} a_{23} a_{31}-a_{12} a_{21} a_{33}\right) x_1 +\left(a_{12} a_{23} a_{32}-a_{12} a_{22} a_{33}\right) x_2 & =a_{12} a_{23} b_3-a_{12} b_2 a_{33} \\ \left(a_{13} a_{21} a_{32}-a_{13} a_{22} a_{31}\right) x_1 +\left(a_{13} a_{23} a_{32}-a_{13} a_{22} a_{33}\right) x_3 & =a_{13} b_2 a_{32}-a_{13} a_{22} b_3 \end{aligned}$

三式相加，得到

$\begin{aligned} &\left(a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}\right. \left.-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}\right) x_1 \\ &=b_1 a_{22} a_{33}+a_{12} a_{23} b_3+a_{13} b_2 a_{32}-a_{13} a_{22} b_3-a_{12} b_2 a_{33}-b_1 a_{23} a_{32} \end{aligned}$

数表：

$\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}$

表达式：$a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$

三阶行列式：$\left|\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|$

利用三阶行列式，等式简记为：

$\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right| x_1=\left|\begin{array}{lll} b_1 & a_{12} & a_{13} \\ b_2 & a_{22} & a_{23} \\ b_3 & a_{32} & a_{33} \end{array}\right|$

同理得到

$\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right| x_2=\left|\begin{array}{lll} a_{11} & b_1 & a_{13} \\ a_{21} & b_2 & a_{23} \\ a_{31} & b_3 & a_{33} \end{array}\right|$

$\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right| x_3=\left|\begin{array}{lll} a_{11} & a_{12} & b_1 \\ a_{21} & a_{22} & b_2 \\ a_{31} & a_{32} & b_3 \end{array}\right|$

若记

$D=\left|\begin{array}{ll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|, \quad D_1=\left|\begin{array}{ll} b_1 & a_{12} & a_{13} \\ b_2 & a_{22} & a_{23} \\ b_3 & a_{32} & a_{33} \end{array}\right|, \quad D_2=\left|\begin{array}{ll} a_{11} & b_1 & a_{13} \\ a_{21} & b_2 & a_{23} \\ a_{31} & b_3 & a_{33} \end{array}\right|, \quad D_3=\left|\begin{array}{ll} a_{11} & a_{12} & b_1 \\ a_{21} & a_{22} & b_2 \\ a_{31} & a_{32} & b_3 \end{array}\right|,$

利用三阶行列式的概念，改写 $x_1$，$x_2$，$x_3$ 的表示：

$x_1=\frac{D_1}{D}, x_2=\frac{D_2}{D}, x_3=\frac{D_3}{D}$

• $D$：系数行列式

---

$\color{green}{行列式按一行展开}$：这里举例按照第一行展开

$\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|=a_{11}\left|\begin{array}{ll} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|-a_{12}\left|\begin{array}{ll} a_{21} & a_{23} \\ a_{31} & a_{33} \end{array}\right|+a_{13}\left|\begin{array}{ll} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right|$

再进行拓展

三阶在空间解析几何中

向量积：$\mathbf{a}=a_1 \mathbf{i}+a_2 \mathbf{j}+a_3 \mathbf{k} \quad \mathbf{b}=b_1 \mathbf{i}+b_2 \mathbf{j}+b_3 \mathbf{k}$

$\begin{aligned} \mathbf{a} \times \mathbf{b}=\left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array}\right| \end{aligned}$

三种表示方法：

$\mathbf{a} \times \mathbf{b}=\left|\begin{array}{cc} a_2 & a_3 \\ b_2 & b_3 \end{array}\right| \mathbf{i}-\left|\begin{array}{cc} a_1 & a_3 \\ b_1 & b_3 \end{array}\right| \mathbf{j}+\left|\begin{array}{cc} a_1 & a_2 \\ b_1 & b_2 \end{array}\right| \mathbf{k}$

$\mathbf{a} \times \mathbf{b}=\left|\begin{array}{ll} a_2 & a_3 \\ b_2 & b_3 \end{array}\right| \mathbf{i}+\left|\begin{array}{ll} a_3 & a_1 \\ b_3 & b_1 \end{array}\right| \mathbf{j}+\left|\begin{array}{cc} a_1 & a_2 \\ b_1 & b_2 \end{array}\right| \mathbf{k}$

$\mathbf{a} \times \mathbf{b}=\left\{\left|\begin{array}{ll} a_2 & a_3 \\ b_2 & b_3 \end{array}\right|,\left|\begin{array}{ll} a_3 & a_1 \\ b_3 & b_1 \end{array}\right|,\left|\begin{array}{ll} a_1 & a_2 \\ b_1 & b_2 \end{array}\right|\right\}$

以上三种表示方式都是正确的

混合积

• $\mathbf{a}=a_1 \mathbf{i}+a_2 \mathbf{j}+a_3 \mathbf{k}=\left\{a_1, a_2, a_3\right\}$
• $\mathbf{b}=b_1 \mathbf{i}+b_2 \mathbf{j}+b_3 \mathbf{k}=\left\{b_1, b_2, b_3\right\}$
• $\mathbf{c}=c_1 \mathbf{i}+c_2 \mathbf{j}+c_3 \mathbf{k}=\left\{c_1, c_2, c_3\right\}$

$\mathbf{b} \times \mathbf{c}=\left\{\left|\begin{array}{ll}b_2 & b_3 \\ c_2 & c_3\end{array}\right|,\left|\begin{array}{ll}b_3 & b_1 \\ c_3 & c_1\end{array}\right|,\left|\begin{array}{ll}b_1 & b_2 \\ c_1 & c_2\end{array}\right|\right\}$

$\begin{aligned} [\mathbf{a} \mathbf{b} \mathbf{c}] \\ &\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})\\ &=\left\{a_1, a_2, a_3\right\} \cdot\left\{\left|\begin{array}{ll} b_2 & b_3 \\ c_2 & c_3 \end{array}\right|,\left|\begin{array}{cc} b_3 & b_1 \\ c_3 & c_1 \end{array}\right|,\left|\begin{array}{cc} b_1 & b_2 \\ c_1 & c_2 \end{array}\right|\right\}\\ &=a_1\left|\begin{array}{ll} b_2 & b_3 \\ c_2 & c_3 \end{array}\right|+a_2\left|\begin{array}{ll} b_3 & b_1 \\ c_3 & c_1 \end{array}\right|+a_3\left|\begin{array}{ll} b_1 & b_2 \\ c_1 & c_2 \end{array}\right|\\ &=\left|\begin{array}{lll} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right| \end{aligned}$

全排列和对换

排列及其逆序数

全排列（排列）：把$n$个不同的元素排成一列

逆序：对于 $n$ 个不同的元素，先规定各元素之间有一个标准次序（例如 $n$ 个不同的自然数，可规定由小到大为标准次序），于是在这 $n$ 个元素的任一排列中，当某一对元素的先后次序与标准次序不同时，就说它构成 $1$ 个逆序。

逆序数：一个排列中所有逆序的总数。

逆序数为奇数的排列叫做奇排列，逆序数为偶数的排列叫做偶排列。

$\color{red}{计算排序的逆序数的方法}$

不失一般性，不妨设 $n$ 个元素为$1$至$n$这$n$个自然数，并规定由小到大为标准次序。设 $p_1p_2...p_n$ 为这$n$个自然数的一个排列，考虑元素 $p_i$（$i= 1 ,2 ,… , n$ ） ，如果比 $p_i$ 大的且排在 $p_i$ 前面的元素有 $t_i$ 个，就说 $p_i$ 这个元素的逆序数是 $t_i$。

排列的逆序数=全体元素的逆序数之总和：$t=t_1+t_2+\cdots+t_n=\sum_{i=1}^n t_i$

对换

对换：在排列中，将任意两个元素对调，其余元素不动。

【定理】一个排列中的任意两个元素兑换，排列改变奇偶性。

证明：

$a_1 \cdots a_l a b b_1 \cdots b_m$

• 相邻对换 $a_1 \cdots a_l a b b_1 \cdots b_m \longrightarrow a_1 \cdots a_l b a b_1 \cdots b_m$
  • $a<b$：$a$的逆序数增加$1$而$b$的逆序数不变
  • $a>b$：$a$的逆序数不变而$b$的逆序数增加$1$
• 一般对换 $a_1 \cdots a_l a b_1 \cdots b_m b c_1 \cdots c_n \longrightarrow a_1 \cdots a_l b b_1 \cdots b_m a c_1 \cdots c_n$
  1. $a_1 \cdots a_l a b_1 \cdots b_m b c_1 \cdots c_n \longrightarrow a_1 \cdots a_l a b b_1 \cdots b_m c_1 \cdots c_n$：$m$次对换
  2. $a_1 \cdots a_l a b b_1 \cdots b_m c_1 \cdots c_n \longrightarrow a_1 \cdots a_l b b_1 \cdots b_m a c_1 \cdots c_n$ ：$m+1$次对换

累计$2m+1$次相邻对换，奇偶性发生变换。

n 阶行列式的定义

回忆三阶行列式

$\begin{aligned} &\left|\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right| \\=& a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31} . \end{aligned}$

任意一项表示为：$a_{1p_1}a_{2p_2}a_{3p_3}$

$(p_1,p_2,p_3)=\{(1,2,3),(2,3,1),(3,1,2),(1,3,2),(2,1,3),(3,2,1)\}$

带正号的三项列标排列是123，231，312；（偶排列）

带负号的三项列标排列是132，213，321。（奇排列）

各项的正负号表示 $(-1)^t$（$t$ 为列标排序的逆序数）

因此改写三阶行列式

$\left|\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|=\sum(-1)^t a_{1 p_1} a_{2 p_2} a_{3 p_3}$

$n$ 阶行列式：

$\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}$

自由组合不同行不同列的$n$个数的乘积，并冠以符号$(-1)^t$并求代数和，得到$n$阶行列式。

按照行顺序：

$\left|\begin{array}{llll} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}\right|=\sum_{p_1, p_2, \ldots, p_n}(-1)^{t} a_{1 p_1} a_{2 p_2} \cdots a_{n p_n}$

按照列顺序：

$\left|\begin{array}{llll} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}\right|=\sum_{p_1, p_2, \ldots, p_n}(-1)^{t} a_{p_1 1} a_{p_2 2} \cdots a_{p_n n}$

任意顺序：

$\left|\begin{array}{llll} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}\right|=\sum(-1)^{t(r_1...r_n)+t(s_1...s_n)} a_{r_1 s_1} a_{r_2 s_2} \cdots a_{r_n s_n}$

记作 $det(a_{ij})$

注：当 $n=1$，一阶行列式 $|a|=a$

主对角行列式：斜边为主对角线。

$\left|\begin{array}{llll} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \dots & \\ & & & \lambda_n \end{array}\right|=\lambda_1 \lambda_2 \cdots \lambda \text {, }$

次对角行列式：斜边为次对角行列式。

$\left|\begin{array}{llll} & & & \lambda_1 \\ & & \lambda_2 & \\ & \dots & & \\ \lambda_n & & & \end{array}\right|=\lambda_1 \lambda_2 \cdots \lambda \text {, }$

行列式的性质

转置行列式：

$D=\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right|$

$D^{T}=\left|\begin{array}{cccc} a_{11} & a_{21} & \cdots & a_{n 1} \\ a_{12} & a_{22} & \cdots & a_{n 2} \\ \vdots & \vdots & & \vdots \\ a_{1 n} & a_{2 n} & \cdots & a_{n n} \end{array}\right|$

【性质1】行列式与它的转置行列式相等。

证明：

$D=det(a_{ij})$ 的转置行列式 $D=det(b_{ji})$，按照行列式的定义：

$D^{\mathrm{T}}=\sum(-1)^t b_{1 p_1} b_{2 p_2} \cdots b_{n p_n}=\sum(-1)^t a_{p_1 1} a_{p_2 2} \cdots a_{p_{n^n}}=D$

【性质2】对换行列式的两行（列），行列式变号。

证明：

$D$ 交换第 $i$ 行与第 $j$ 列得到 $D_1$

$D=\left|\begin{array}{ccccc} \ldots & \ldots & \ldots & \ldots & \ldots \\ \ldots & x & \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots & y & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots \end{array}\right|$

$D^{\prime}=\left|\begin{array}{ccccc} \ldots & \ldots & \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots & y & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ \ldots & x & \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots \end{array}\right|$

任取 $D$ 中的一项：$a_{1 p_1} \ldots a_{i p_i} \ldots a_{j p_j} \ldots a_{n p_n}=a_{1 p_1} \ldots x \ldots y \ldots a_{n p_n}$，符号为 $(-1)^{\tau\left(p_1 \ldots p_i \ldots p_j \ldots p_n\right)}$。

这一项在 $D^{\prime}$ 中：$a_{1 p_1} \ldots x \ldots y \ldots a_{n p_n}=b_{1 p_1} \ldots b_{j p_i} \ldots b_{i p_j} \ldots b_{n p_n}=b_{1 p_1} \ldots b_{i p_j} \ldots b_{j p_i} \ldots b_{n p_n}$，符号为 $(-1)^{\tau\left(p_1 \ldots p_j \ldots p_i \ldots p_n\right)}==-(-1)^{\tau\left(p_1 \ldots p_i \cdots p_j \ldots p_n\right)}$。

得到这一项在 $D^{\prime}$ 和 $D$ 中所带符号相反。

这里为任意所取的一项，那么所有对应项所带符号恰好相反。

所以 $D^{\prime}=D$。

【推论】

• 奇数次互换行列式的两行(两列)，行列式变号。

• 偶数次互换行列式的两行(两列)，行列式不变。

【推论】如果行列式有两行(列)完全相同，则此行列式等于零。

【性质3】行列式的某一行（列）中所有的元素都乘以同一数 $k$，等于用数 $k$ 乘此行列式。

证明：

$\left|\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1 n} \\ \ldots & \ldots & \ldots & \ldots \\ k a_{i 1} & k a_{i 2} & \ldots & k a_{i n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}\right|=\sum(-1)^{\tau\left(p_1 p_2 \ldots p_n\right)} a_{1 p_1 } \cdots \left(k a_{i p_i}\right) \cdots a_{n p_n}=k \sum(-1)^{\tau\left(p_1 p_2 \cdots p_n\right)} a_{1 p_1} \cdots a_{i p_i} \cdots a_{n p_n}=KD$

【推论】

• 行列式中某一行（列）的公因子可以提到行列式外。

• 可以将行列式外的乘积因子乘到行列式的某一行（列）。

【性质4】行列式中如果有两行（列）元素成比例，则此行列式等于零。

【性质5】若行列式的某一行（列）的元素都是两数之和，例如第 $i$ 行的元素都是两数之和：

$D=\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ \vdots & \vdots & & \vdots \\ b_{i 1}+c_{i 1} & b_{i 2}+c_{i 2} & \cdots & b_{i n}+c_{i n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right|$

则 $D$ 等于下列两个行列式之和：

$D=\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ \vdots & \vdots & & \vdots \\ b_{i 1} & b_{i 2} & \cdots & b_{i n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right|+\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ \vdots & \vdots & & \vdots \\ c_{i 1} & c_{i 2} & \cdots & c_{i n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right|$

证明：

$D=\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ \vdots & \vdots & & \vdots \\ b_{i 1}+c_{i 1} & b_{i 2}+c_{i 2} & \cdots & b_{i n}+c_{i n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right| \\ \begin{aligned} = & \sum(-1)^{\tau\left(p_1 p_2 \cdots p_n\right)} a_{1 p_1} \ldots\left(b_{i p_i}+c_{i p_i}\right) \cdots a_{n p_n} \\ \\ = & \sum(-1)^{\tau\left(p_1 p_2 \cdots p_n\right)} a_{1 p_1} \ldots b_{i p_i} \cdots a_{n p_n}+\sum(-1)^{\tau\left(p_1 p_2 \cdots p_n\right)} a_{1 p_1} \ldots c_{i p_i} \cdots a_{n p_n} \\ \\ = & D_1+D_2 \end{aligned}$

性质3和性质5统称为行列式的线性性质（线性运算）。

【性质6】把行列式的某一行（列）的各元素乘以同样数然后加到另一行（列）对应的元素上去，行列式不变。

证明：利用【性质4】和【性质5】可以推出来。

行列式按一行（列）展开

余子式：在 $n$ 阶行列式中，把元素 $a_{ij}$ 所在的第 $i$ 行和第 $j$ 列划去后，留下来的 $n-1$ 阶行列式称为元素 $a_{ij}$ ，记作 $M_{ij}$。

代数余子式：$(-1)^{i+j}M_{ij}$，记作 $A_{ij}$。

【定理】行列式等于它的某一行（列）的所有元素与它们对应的代数余子式的乘积之和。

【引理】设 $n$ 阶行列式 $D$ 的第 $i$ 行, 除 $a_{i j}$ 外都为零, 则 $D=a_{i j} A_{i j}$。

• 按第 $i$ 行展开：

$D=a_{i 1} A_{i 1}+a_{i 2} A_{i 2}+\ldots+a_{i n} A_{i n}$

• 按第 $j$ 列展开：

$D=a_{1 j} A_{1 j}+a_{2 j} A_{2 j}+\ldots+a_{n j} A_{n j}$

【命题】行列式某一行（列）的各元素与另一行（列）对应元素的代数余子式的乘积之和等于 $0$。

• 按第 $i$ 行展开：

$a_{i 1} A_{j 1}+a_{i 2} A_{j 2}+\ldots+a_{i n} A_{j n}=0 \quad(j \neq i)$

• 按第 $j$ 列展开：

$a_{1 i} A_{1 j}+a_{2 i} A_{2 j}+\ldots+a_{n i} A_{n j}=0(j \neq i)$

将【定理】和【命题】统一表示：

$a_{i 1} A_{j 1}+a_{i 2} A_{j 2}+\ldots+a_{i n} A_{j n}=\left\{\begin{array}{l} D, j=i \\ 0, j \neq i \end{array}\right.$

范德蒙行列式：

$V_n=\left|\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ x_1 & x_2 & x_3 & \cdots & x_n \\ x_1^2 & x_2^2 & x_3^2 & \cdots & x_n^2 \\ \vdots & \vdots & \vdots & & \vdots \\ x_1^{n-2} & x_2^{n-2} & x_3^{n-2} & \cdots & x_n^{n-2} \\ x_1^{n-1} & x_2^{n-1} & x_3^{n-1} & \cdots & x_n^{n-1} \end{array}\right|$

$V_2=\left|\begin{array}{cc}1 & 1 \\ x_1 & x_2\end{array}\right|=x_2-x_1$

假设等式对于 $n-1$ 有 $V_{n-1}=\prod_{n \geq i>j \geq 2}\left(x_i-x_j\right)$

从最后一行起，依次用下一行减去上一行的 $x_1$ 倍

$V_n=\left|\begin{array}{ccccc}1 & 1 & 1 & \cdots & 1 \\ 0 & x_2-x_1 & x_3-x_1 & \cdots & x_n-x_1 \\ 0 & x_2^2-x_1 x_2 & x_3^2-x_1 x_3 & \cdots & x_n^2-x_1 x_n \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & x_2^{n-2}-x_1 x_2^{n-3} & x_3^{n-2}-x_1 x_3^{n-3} & \cdots & x_n^{n-2}-x_1 x_n^{n-3} \\ 0 & x_2^{n-1}-x_1 x_2^{n-2} & x_3^{n-1}-x_1 x_3^{n-2} & \ldots & x_n^{n-1}-x_1 x_n^{n-2}\end{array}\right|$

用上述【定理】，

$V_n =\left|\begin{array}{cccc}x_2-x_1 & x_3-x_1 & \cdots & x_n-x_1 \\ x_2^2-x_1 x_2 & x_3^2-x_1 x_3 & \cdots & x_n^2-x_1 x_n \\ \vdots & \vdots & & \vdots \\ x_2^{n-2}-x_1 x_2^{n-3} & x_3^{n-2}-x_1 x_3^{n-3} & \cdots & x_n^{n-2}-x_1 x_n^{n-3} \\ x_2^{n-1}-x_1 x_2^{n-2} & x_3^{n-1}-x_1 x_3^{n-2} & \ldots & x_n^{n-1}-x_1 x_n^{n-2}\end{array}\right|$

$V_n =\left(x_2-x_1\right)\left(x_3-x_1\right) \cdots\left(x_n-x_1\right)\left|\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ x_2 & x_3 & \cdots & x_n \\ \vdots & \vdots & & \vdots \\ x_2^{n-3} & x_3^{n-3} & \cdots & x_n^{n-3} \\ x_2^{n-2} & x_3^{n-2} & \cdots & x_n^{n-2} \end{array}\right|$

即：

$\begin{aligned} V_{n} & =\left(x_2-x_1\right)\left(x_3-x_1\right) \cdots\left(x_n-x_1\right)V_{n-1} \\ & = \left(x_2-x_1\right)\left(x_3-x_1\right) \ldots\left(x_n-x_1\right) \prod_{n \geq i>j \geq 2}\left(x_i-x_j\right) \\ & = \prod_{n \geq i \geq 2}\left(x_i-x_1\right) \cdot \prod_{n \geq i>j \geq 2}\left(x_i-x_j\right) \\ & = \prod_{n \geq i>j \geq 1}\left(x_i-x_j\right) \end{aligned}$

行列式按 k 行（列）展开

子式：设 $D$ 是 $n$ 阶行列式，在 $D$ 中任意选定 $k$ 行 $k$ 列（$1 \leqslant k \leqslant n$），则位于这些行和列的交叉上的 $k^2$ 个元素按照原来位置组成的 $k$ 阶行列式 $M$ 称为 $D$ 的一个 $k$ 阶子式。

子式的余子式：在 $D$ 中划去上述 $k$ 行 $k$ 列后余下的元素按照原来的位置组成的 $n-k$ 阶行列式 $M^{\prime}$ 称为 $D$ 的一个 $k$ 阶子式 $M$ 的余子式。

代数余子式：设 $M$ 由 $D$ 中的第 $i_1, i_2, \ldots, i_k$ 行和第 $j_1, j_2, \ldots, j_k$ 的元素构成的 $k$ 阶子式，$M^{\prime}$ 是 $M$ 的余子式，则

$A=(-1)^{\left(i_1+i_2+\ldots+i_k\right)+\left(j_1+j_2+\ldots+j_k\right)} M^{\prime}$

称为 $D$ 的一个 $k$ 阶子式 $M$ 的代数余子式。

【定理】拉普拉斯定理：设在 $n$ 阶行列式 $D$ 中任意取定 $k$ 行（$1 \leqslant k \leqslant n$），则由这 $k$ 行元素所组成的一切 $k$ 阶子式与它们的代数余子式的乘积之和等于行列式 $D$。

行列式的翻转与旋转

$D=\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array}\right|$

上下翻转：

$D_u=\left|\begin{array}{cccc} a_{n1} & a_{n2} & \cdots & a_{n n} \\ a_{n-1,1} & a_{n-1,2} & \cdots & a_{n-1,n} \\ \vdots & \vdots & & \vdots \\ a_{11} & a_{12} & \cdots & a_{1n} \end{array}\right|$

有：

$D_u=(-1)^\frac{n(n-1)}{2}D$

左右翻转：

$D_l=\left|\begin{array}{cccc} a_{1n} & a_{1,n-1} & \cdots & a_{11} \\ a_{2n} & a_{2,n-1} & \cdots & a_{21} \\ \vdots & \vdots & & \vdots \\ a_{nn} & a_{n,n-1} & \cdots & a_{n1} \end{array}\right|$

有：

$D_l=(-1)^\frac{n(n-1)}{2}D$

主对角线翻转：转置

$D^T=\left|\begin{array}{cccc} a_{11} & a_{21} & \cdots & a_{n1} \\ a_{12} & a_{22} & \cdots & a_{n2} \\ \vdots & \vdots & & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{nn} \end{array}\right|$

有：

$D^T=D$

次对角线翻转：

$D_s=\left|\begin{array}{cccc} a_{nn} & a_{n-1,n} & \cdots & a_{1n} \\ a_{n,n-1} & a_{n-1,n-1} & \cdots & a_{1,n-1} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n-1,1} & \cdots & a_{11} \end{array}\right|$

有：

$D_s$ 经过上下翻转和左右翻转得到 $D^T$

$D_s=(-1)^\frac{n(n-1)}{2}(-1)^\frac{n(n-1)}{2}D^T=D^T=D$

逆时针旋转 $90^{\circ}$：

$D_{90}=\left|\begin{array}{cccc} a_{1n} & a_{2n} & \cdots & a_{nn} \\ a_{1,n-1} & a_{2,n-1} & \cdots & a_{n,n-1} \\ \vdots & \vdots & & \vdots \\ a_{11} & a_{21} & \cdots & a_{n1} \end{array}\right|$

有：

$D_{90}$ 经过转置，左右翻转得到 $D$

$D_{90}=(-1)^\frac{n(n-1)}{2}D$

逆时针旋转 $180^{\circ}$：

$D_{180}=\left|\begin{array}{cccc} a_{nn} & a_{n,n-1} & \cdots & a_{n1} \\ a_{n-1,n} & a_{n-1,n-1} & \cdots & a_{n-1,1} \\ \vdots & \vdots & & \vdots \\ a_{1n} & a_{1,n-1} & \cdots & a_{11} \end{array}\right|$

有：

$D_{90}$ 逆时针旋转 $90^{\circ}$ 得到 $D_{180}$

$D_{180}=(-1)^\frac{n(n-1)}{2}D_{90}=(-1)^\frac{n(n-1)}{2}(-1)^\frac{n(n-1)}{2}D=D$

顺时针旋转 $90^{\circ}$：

$D_{90}^{\prime}$ 是 $D$ 顺时针旋转 $90^{\circ}$ 得到的，换言之，$D$ 是 $D_{90}^{\prime}$ 逆时针旋转 $90^{\circ}$ 得到的。

$D=(-1)^\frac{n(n-1)}{2}D_{90}^{\prime}$

$(-1)^\frac{n(n-1)}{2}D=(-1)^\frac{n(n-1)}{2}(-1)^\frac{n(n-1)}{2}D_{90}^{\prime}$

$D_{90}^{\prime}=(-1)^\frac{n(n-1)}{2}D$

顺时针旋转 $180^{\circ}$：

同上可得：

$D_{180}^{\prime}=D$

操作	关系
上下翻转	$D_u=(-1)^\frac{n(n-1)}{2}D$
左右翻转	$D_l=(-1)^\frac{n(n-1)}{2}D$
主对角线翻转	$D^T=D$
次对角线翻转	$D_s=D$
逆时针旋转 $90^{\circ}$	$D_{90}=(-1)^\frac{n(n-1)}{2}D$
逆时针旋转 $180^{\circ}$	$D_{180}=D$
顺时针旋转 $90^{\circ}$	$D_{90}^{\prime}=(-1)^\frac{n(n-1)}{2}D$
顺时针旋转 $180^{\circ}$	$D_{180}^{\prime}=D$

计算行列式

行列式的计算

意义	记号	行列式
交换 $i$ 和 $j$ 两行	$r_i \leftrightarrow r_j$	行列式变号
第 $i$ 行乘以 $k$	$r_i \times k$	行列式乘以 $k$
第 $j$ 行乘以 $k$ 加到第 $i$ 行	$r_i+k r_j$	行列式不变
交换 $i$ 和 $j$ 两列	$c_i \leftrightarrow c_j$	行列式变号
第 $i$ 列乘以 $k$	$c_i \times k$	行列式乘以 $k$
第 $j$ 列乘以 $k$ 加到第 $i$ 列	$c_i+k c_j$	行列式不变

对应上述【性质2】，【性质3】和【性质5】

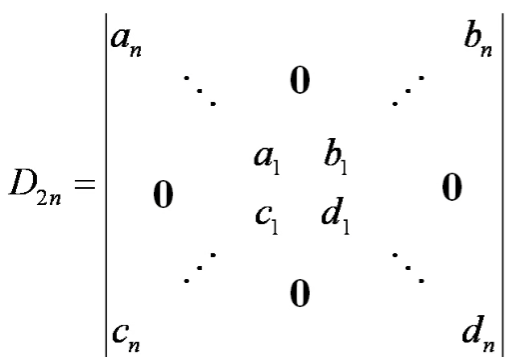
爪型行列式：

$D=\left|\begin{array}{cccc} a_0 & b_1 & b_2 & \cdots & b_n \\ d_1 & a_1 & & \\ d_2 & & a_2 & \\ \vdots & & & \ddots & \\ d_n & & & & a_n \end{array}\right|$

其余元素均为 $0$。

经过 $c_1-\frac{d_j}{a_j}$，$j=2,\cdots,n$，

得到

$D=\left|\begin{array}{cccc} a_0-\frac{d_1}{a_1} b_1-\cdots-\frac{d_n}{a_n} b_n & b_1 & b_2 & \cdots & b_n \\ 0 & a_1 & & \\ 0 & & a_2 & \\ \vdots & & & \ddots & \\ 0 & & & & a_n \end{array}\right|$

因此

$D=\left(a_0-\frac{d_1}{a_1} b_1-\cdots-\frac{d_n}{a_n} b_n\right) a_1 a_2 \cdots a_n$

分块行列式：可用范德蒙行列式或拉普拉斯定理推导。

$\left|\begin{array}{ll} A & 0 \\ C & B \end{array}\right|=|A||B|$

 

解：

取第 $1$ 行和第 $2n$ 行，只有一个非零子式：

$M=\left|\begin{array}{ll} a_n & b_n \\ c_n & d_n \end{array}\right|$

$M$ 的余子式：$M^{\prime}=D_{2(n-1)}$

$M$ 的代数余子式：$A=(-1)^{(1+2 n)+(1+2 n)}M^{\prime}=(-1)^{(1+2 n)+(1+2 n)}D_{2(n-1)}=D_{2(n-1)}$

根据【定理】拉普拉斯定理

$D_{2 n}=M A=\left|\begin{array}{ll} a_n & b_n \\ c_n & d_n \end{array}\right| D_{2(n-1)}$

递归公式：

$\begin{aligned} D_{2 n}& =\left|\begin{array}{cc} a_n & b_n \\ c_n & d_n \end{array}\right| D_{2(n-1)} \\ & =\left|\begin{array}{ll} a_n & b_n \\ c_n & d_n \end{array}\right| \cdot\left|\begin{array}{cc} a_{n-1} & b_{n-1} \\ c_{n-1} & d_{n-1} \end{array}\right| D_{2(n-2)} \\ & =\left|\begin{array}{cc} a_n & b_n \\ c_n & d_n \end{array}\right| \cdot\left|\begin{array}{cc} a_{n-1} & b_{n-1} \\ c_{n-1} & d_{n-1} \end{array}\right| \ldots\left|\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array}\right| D_2 \\ & =\left|\begin{array}{ll} a_n & b_n \\ c_n & d_n \end{array}\right| \cdot\left|\begin{array}{cc} a_{n-1} & b_{n-1} \\ c_{n-1} & d_{n-1} \end{array}\right| \ldots\left|\begin{array}{cc} a_2 & b_2 \\ c_2 & d_2 \end{array}\right|\left|\begin{array}{cc} a_1 & b_1 \\ c_1 & d_1 \end{array}\right| \\ \end{aligned}$

故

$\begin{aligned} D_{2n} & = \left(a_{n-1} d_{n-1}-b_{n-1} c_{n-1}\right) \cdots\left(a_1 d_1-b_1 c_1\right) \\ & =\prod_{i=1}^n\left(a_i d_i-b_i c_i\right) \end{aligned}$

下三角行列式：斜边为主对角线，上角均为 $0$。

$D=\left|\begin{array}{cccc} a_{11} & & & \\ a_{21} & a_{22} & & 0 \\ \vdots & \vdots & \ddots & \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right|=a_{11} a_{22} \cdots a_{n n}$

左右翻转，得到斜边为次对角线，上角均为 $0$ 的次下三角行列式。

$D^{\prime}=(-1)^\frac{n(n-1)}{2}D$

克拉默法则

$\left\{\begin{array}{c} a_{11} x_1+a_{12} x_2+\ldots+a_{1 n} x_n=b_1 \\ a_{21} x_1+a_{22} x_2+\ldots+a_{2 n} x_n=b_2 \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ a_{n 1} x_1+a_{n 2} x_2+\ldots+a_{n n} x_n=b_n \end{array}\right.$

$D=\left|\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}\right| \neq 0$

如果线性方程组的系统行列式不等于 $0$，则线性方程组有唯一解。

$x_1=\frac{D_1}{D}, x_2=\frac{D_2}{D}, \cdots, x_n=\frac{D_n}{D}$

其中 $D_j$，$j=1,\cdots,n$

$D_j=\left|\begin{array}{ccccccc} a_{11} & \cdots & a_{1, j-1} & b_1 & a_{1, j+1} & \cdots & a_{1 n} \\ a_{21} & \cdots & a_{2, j-1} & b_2 & a_{2, j+1} & \cdots & a_{2 n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n 1} & \cdots & a_{n, j-1} & b_n & a_{n, j+1} & \cdots & a_{n n} \end{array}\right|$

证明：

1. 先证 $x_1=\frac{D_1}{D}, x_2=\frac{D_2}{D}, \cdots, x_n=\frac{D_n}{D}$ 是方程组的解。

只需验证满足第 $i$ 个方程，即

$a_{i 1} x_1+a_{i 2} x_2+\ldots+a_{i n} x_n=b_i$

也即

$a_{i 1} \frac{D_1}{D}+a_{i 2} \frac{D_2}{D}+\ldots+a_{i n} \frac{D_n}{D}=b_i$

设 $A_{ij}$，$i=1,\cdots,n$ 是 $D_j$ 的关于第 $j$ 列的代数余子式

$D_j=b_1 A_{1 j}+b_2 A_{2 j}+\ldots+b_n A_{n j},j=1,\cdots,n$

上式左端

$\begin{aligned} \text { 左端 }= & \frac{1}{D}\left(a_{i 1} D_1+a_{i 2} D_2+\cdots+a_{i n} D_n\right)\\ = &\frac{1}{D}[a_{i 1}\left(b_1 A_{11}+b_2 A_{21}+\cdots+b_n A_{n 1}\right) + a_{i 2}\left(b_1 A_{12}+b_2 A_{22}+\cdots+b_n A_{n 2}\right)+\cdots + a_{i n}\left(b_2 A_{1n}+b_2 A_{2n}+\cdots+b_n A_{n n}\right)] \\ = & \frac{1}{D}[b_1\left(a_{i 1} A_{11}+a_{i 2} A_{12}+\cdots+a_{i n} A_{1 n}\right) +b_2\left(a_{i 1} A_{21}+a_{i 2} A_{22}+\cdots+a_{i n} A_{2 n}\right)+\cdots + b_i\left(a_{i 1} A_{i1}+a_{i 2} A_{i2}+\cdots+a_{i n} A_{i n}\right)+\cdots + b_n\left(a_{i 1} A_{n1}+a_{i 2} A_{n2}+\cdots+a_{i n} A_{n n}\right) \end{aligned}$

又（考虑第 $D$ 的 第 $i$ 行）

$a_{i 1} A_{j 1}+a_{i 2} A_{j 2}+\ldots+a_{i n} A_{j n}=\left\{\begin{array}{l} D,j=i \\ 0,j \neq i \end{array}\right.$

$\begin{aligned} \text { 左端 }= \frac{1}{D}[0+0+\cdot+D+\cdots+0]=\frac{1}{D} b_i D=b_i=\text { 右端 } \end{aligned}$

所以 $x_j$（$j=1,2,\cdots,n$）验证满足第 $i$ 个方程（$i=1,2,\cdots,n$）。

2. 再来证明解的唯一性

设 $x_j=c_j$（$j=1,2,\cdots,n$）满足

$\left\{\begin{array}{c} a_{11} c_1+a_{12} c_2+\cdots+a_{1 n} c_n=b_1 \\ a_{21} c_1+a_{22} c_2+\cdots+a_{2 n} c_n=b_2 \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ a_{n 1} c_1+a_{n 2} c_2+\cdots+a_{n n} c_n=b_n \end{array}\right.$

只需证明：$c_1=\frac{D_1}{D}, c_2=\frac{D_2}{D}, \cdots, c_n=\frac{D_n}{D}$

用 $D$ 的第 $j$ 列元素的代数余子式 $A_{ij}$，$i=1,\cdots,n$ 分别乘以以上等式两端，得

$\left\{\begin{array}{c} (a_{11} c_1+a_{12} c_2+\cdots+a_{1 n} c_n)A_{1 j}=b_1A_{1 j} \\ (a_{21} c_1+a_{22} c_2+\cdots+a_{2 n} c_n)A_{2 j}=b_2A_{2 j} \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ (a_{n 1} c_1+a_{n 2} c_2+\cdots+a_{n n} c_n)A_{n j}=b_nA_{n j} \end{array}\right.$

所以方程两端相加

$\begin{aligned} \left(a_{11} A_{1 j}+a_{21} A_{2 j}+\ldots+a_{n 1} A_{n j}\right) c_1 +\cdots+\left(a_{1j} A_{1 j}+a_{2j} A_{2 j}+\ldots+a_{n j} A_{n j}\right) c_j+\cdots+\left(a_{1n} A_{1 j}+a_{2n} A_{2 j}+\ldots+a_{n n} A_{n j}\right) c_n=b_1 A_{1 j}+b_2 A_{2 j}+\ldots+b_n A_{n j} \end{aligned}$

又（考虑第 $D$ 的 第 $i$ 列）

$a_{1 i} A_{1 j}+a_{2 i} A_{2 j}+\ldots+a_{n i} A_{n j}=\left\{\begin{array}{l} D,j=i \\ 0,j \neq i \end{array}\right.$

$0 \cdot c_1+\cdots+D \cdot c_j +\cdots+0 \cdot c_n=b_1 A_{1 j}+b_2 A_{2 j}+\ldots+b_n A_{n j}$

$D c_j=D_j$

$c_j=\frac{D_j}{D} \quad(j=1,2, \ldots, n)$

得证！

克拉默法则的应用及线性方程组解的讨论

微积分

在由方程组所确定的隐函数的微分运算中，常常用克拉默法则，来求隐函数的导数和偏导数。

设方程组 $\left\{\begin{array}{l}x=e^u+u \sin v \\ y=e^u-u \cos v\end{array}\right.$ 确定了两个二元函数 $\left\{\begin{array}{l}u=u(x, y) \\ v=v(x, y)\end{array}\right.$，求偏导数 $\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}$。

解：

方程组两边对 $x$ 求偏导

$\left\{\begin{aligned} & 1=e^u \frac{\partial u}{\partial x}+\frac{\partial u}{\partial x} \sin v+u \cos v \frac{\partial v}{\partial x} \\ & 0=e^u \frac{\partial u}{\partial x}-\frac{\partial u}{\partial x} \cos v+u \sin v \frac{\partial v}{\partial x} \end{aligned}\right.$

$\left\{\begin{array}{l} \left(e^u+\sin v\right) \frac{\partial u}{\partial x}+u \cos v \frac{\partial v}{\partial x}=1 \\ \left(e^u-\cos v\right) \frac{\partial u}{\partial x}+u \sin v \frac{\partial v}{\partial x}=0 \end{array}\right.$

• $\frac{\partial u}{\partial x}=\frac{\left|\begin{array}{ll}1 & u \cos v \\ 0 & u \sin v\end{array}\right|}{\left|\begin{array}{ll}e^u+\sin v & u \cos v \\ e^u-\cos v & u \sin v\end{array}\right|}=\frac{\sin v}{1+e^u(\sin v-\cos v)}$
• $\frac{\partial v}{\partial x}=\frac{\left|\begin{array}{ll}e^u+\sin v & 1 \\ e^u-\cos v & 0\end{array}\right|}{\left|\begin{array}{ll}e^u+\sin v & u \cos v \\ e^u-\cos v & u \sin v\end{array}\right|}=\frac{\cos v-e^u}{u\left[1+e^u(\sin v-\cos v)\right]}$

多项式插值与插值曲线

插值多项式：设 ($x_i,y_i$),（$i=1,\cdots,n+1$）是 $n+1$ 个横坐标不同的点，则有唯一的次数不超过 $n$ 次的多项式：

$p(x)=a_0+a_1 x+a_2 x^2+\ldots+a_n x^n$

满足 $p(x_i)=y_i$，（$i=1,\cdots,n+1$）

插值曲线：有唯一次数不超过 $n$ 次的曲线 $y=a_0+a_1 x+a_2 x^2+\ldots+a_n x^n$ 经过上述给定的 $n+1$ 个点。

证明：

把 $n+1$ 个点带入方程，得到以 $a_0,a_1,\cdots,a_n$ 为未知数的线性方程组：

$\left\{\begin{array}{c} a_0+a_1 x_1+\ldots+a_n x_1^n=y_1 \\ a_0+a_1 x_2+\ldots+a_n x_2^n=y_2 \\ \ldots \ldots \ldots \ldots \ldots \ldots \\ a_0+a_1 x_{n+1}+\ldots+a_n x_{n+1}^n=y_{n+1} \end{array}\right.$

系数行列式 $D$：

$D=\left|\begin{array}{cccc} 1 & x_1 & \cdots & x_1^n \\ 1 & x_2 & \cdots & x_2^n \\ \cdots & \cdots & \cdots & \cdots \\ 1 & x_{n+1} & \cdots & x_{n+1}^n \end{array}\right|=\prod_{j<i}\left(x_i-x_j\right) \neq 0$

方程组有唯一的解：$a_i=\frac{D_{i}}{D} \quad(j=0,1, \ldots, n+1)$

$p(x)=\frac{1}{D}\left(D_1+D_2 x+D_3 x^2+\ldots+D_{n+1} x^n\right)$