深度模型优化与正则化

优化问题：

神经网络模型是非凸函数，且存在梯度消失原因
深度神经网络模型参数较多

泛化问题（正则化）：训练数据集产生过拟合，需要通过正则化来改进泛化能力。

网络优化

网络优化目标：期望风险，最小化取自数据生成分布数据的预测误差期望。

J(\theta)=E_{(\mathbf{x}, \mathbf{y}): p_{\text {data }}}[L(f(\mathbf{x} ; \theta), \mathbf{y})]

又通常 $p_{\text {data }}$ 未知，故近似用训练集中的样本替代： $p_{\text {data }} \approx \hat{p}_{\text {data }}$

得到经验风险，并使其最小化：

E_{(\mathbf{x}, \mathbf{y})}: \hat{p}_{\text {data }}[L(f(\mathbf{x} ; \theta), \mathbf{y})]=\frac{1}{N} \sum_{i=1}^N L\left(f\left(\mathbf{x}^{(i)} ; \theta\right), y^{(i)}\right)

网络结构多样性：超参数较多
非凸优化问题：初始化参数、陷入局部最优点

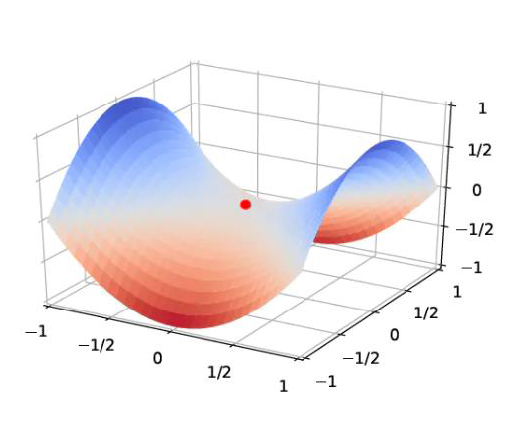
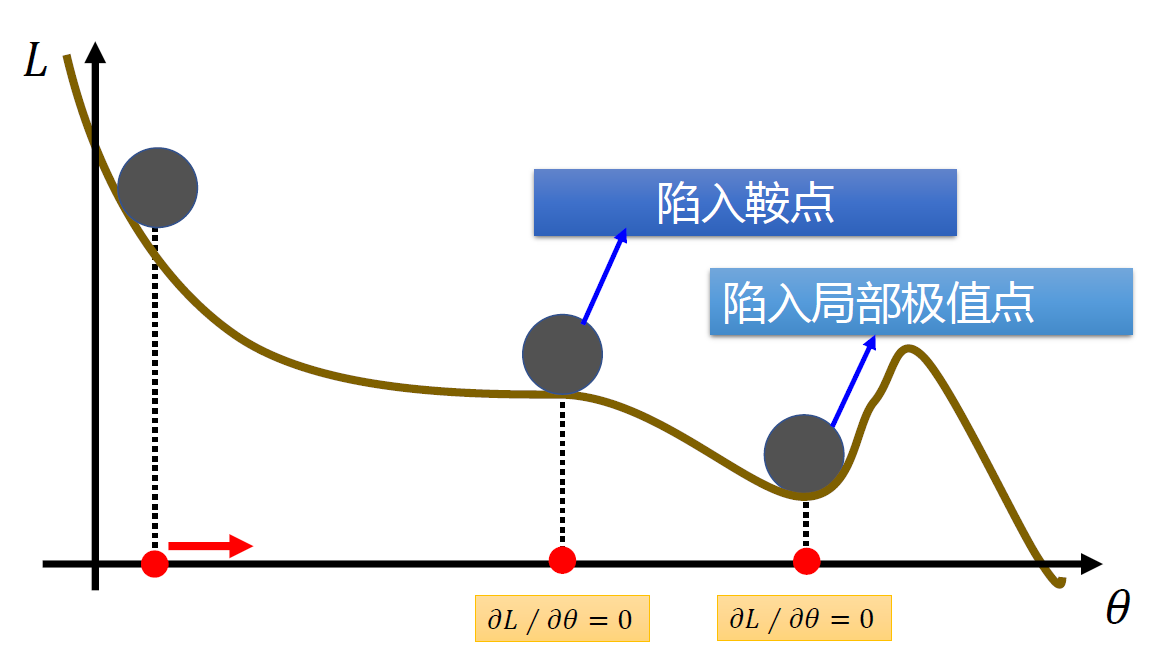
非凸优化问题在高维空间中，非凸优化最大的难点不在于如何逃离局部最优点，而是如何逃离鞍点。

一阶导数： $\nabla L(\theta)=0$

二阶导数： $\nabla^2 L(\theta)$

$\nabla^2 L(\theta)=0$ ，驻点
$\nabla^2 L(\theta)$ 所有特征值为正，为局部最小点
$\nabla^2 L(\theta)$ 所有特征值为负，为局部最大点
$\nabla^2 L(\theta)$ 所有特征值有正有负，为鞍点

在高维空间中，局部最小值（Local Minima）要求在每一维度上都是最低点，这种概率非常低。也就说是，高维空间中大部分驻点都是鞍点。

==网络结构多样性==：

寻找高效的，稳定的优化方法
超参数比较多
- 超参数优化

==非凸优化问题==：

逃离局部最优
- 自适应学习率

批量

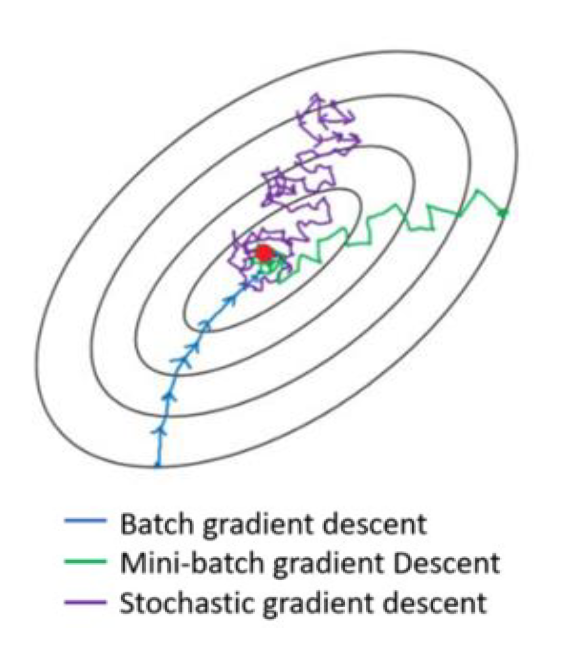
批量梯度下降

批量梯度下降（Batch Gradient Descent）：每次更新都使用整个训练集数据，需要较多计算资源。

$\theta^0$
计算 $\theta^0$ 梯度 $\nabla L\left(\theta^0\right)$ ，更新 $\theta^1=\theta^0-\alpha \nabla L\left(\theta^0\right)$
计算 $\theta^1$ 梯度 $\nabla L\left(\theta^1\right)$ ，更新 $\theta^2=\theta^1-\alpha \nabla L\left(\theta^1\right)$
$\cdots$
停止迭代直到 $\nabla L\left(\theta^t\right)=0$

\nabla L(\theta)=\frac{1}{N} \sum_{n=1}^N \nabla L\left(f\left(\mathbf{x}^{(n)} ; \theta\right), y^{(n)}\right)

随机梯度下降

随机梯度下降（Stochastic Gradient Descent）：每次只取一个样本（编号为 $n$ ）计算梯度。

\nabla L(\theta)=\nabla L\left(f\left(\mathbf{x}^{(n)} ; \theta\right), y^{(n)}\right)

小批量梯度下降

小批量梯度下降（Mini-batch Gradient Descent）：

选取包含 $k$ 个样本的小批量样本集 $S^t$ ：处理同批量梯度下降
$\mathbf{g}^t=\nabla L\left(\theta^{t-1}\right)$
$\theta^t=\theta^{t-1}-\alpha \mathbf{g}^t$ $θ^{t} = θ^{t - 1} - α g^{t}$
1. $\theta^0$
2. 计算 $\theta^0$ 梯度 $\nabla L\left(\theta^0\right)$ ，更新 $\theta^1=\theta^0-\alpha \nabla L\left(\theta^0\right)$
3. 计算 $\theta^1$ 梯度 $\nabla L\left(\theta^1\right)$ ，更新 $\theta^2=\theta^1-\alpha \nabla L\left(\theta^1\right)$
4. $\cdots$
5. 计算 $\theta^{t-1}$ 梯度 $\nabla L\left(\theta^{t-1}\right)$ ，更新 $\theta^t=\theta^{t-1}-\alpha \nabla L\left(\theta^{t-1}\right)$

\nabla L(\theta)=\frac{1}{K} \sum_{(\mathbf{x}, y) \in S^t} \nabla L(f(\mathbf{x} ; \theta), y)

一般而言，批量（Batch Size）大小不影响梯度的期望，但是会影响梯度的方差。

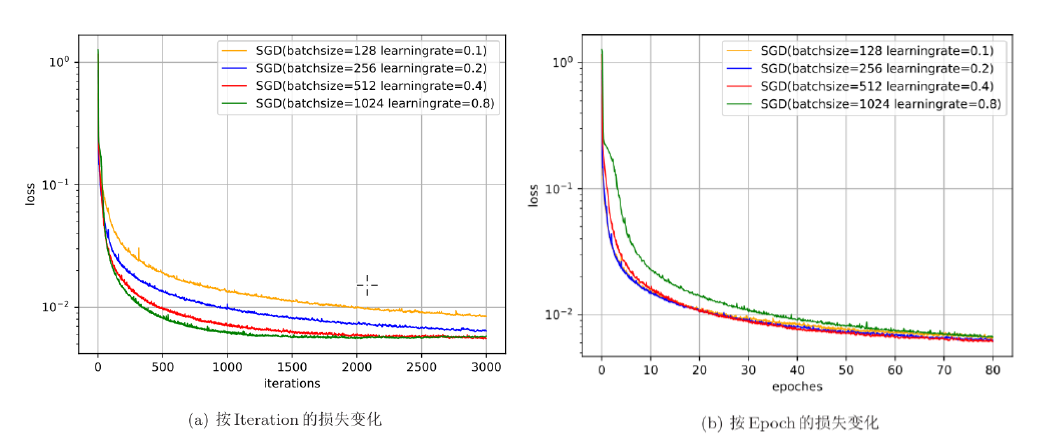
$\text {Epoch}$ ：训练样本训练次数
$\text {Iteration}$ ：单个 $\text {Epoch}$ 包含多次迭代

\text {Iteration}=\frac{\text {训练样本的数量 } N}{\text {批量大小 }K}

批量越大，可以设置较大的学习率；批量越小，可以设置较小的学习率。

学习率与梯度

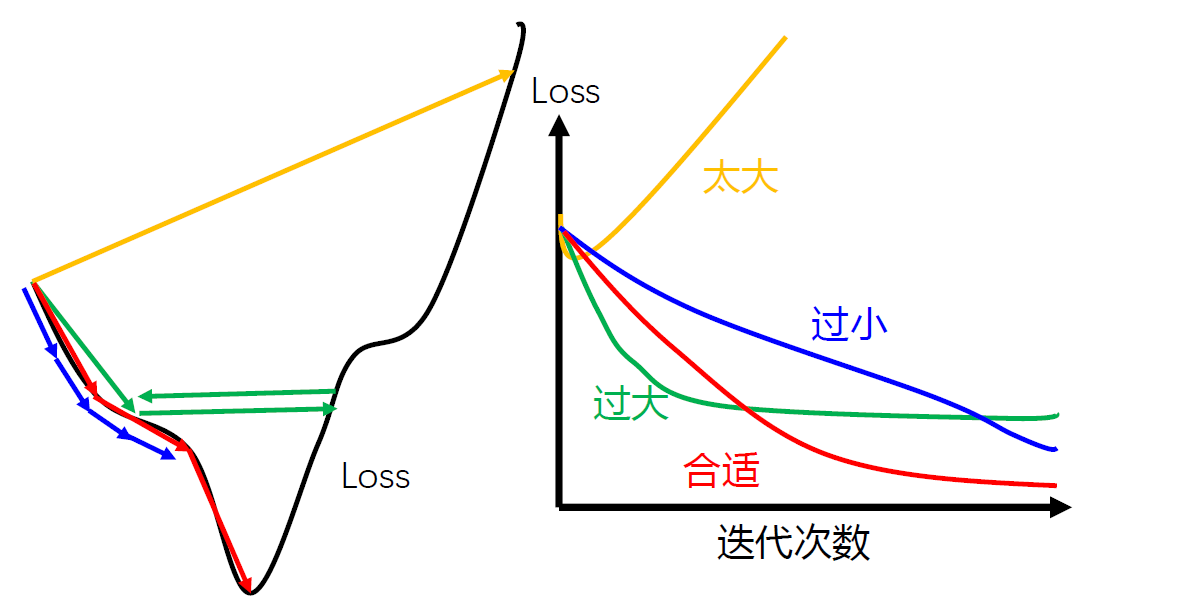
学习率

\theta^t=\theta^{t-1}-\alpha \mathbf{g}^t

学习率衰减

==开始时，距离极值点远，保持更大保证收敛速度。迭代多次，接近极值点处，保持较小避免来回震荡。==

学习率衰减（Learning Rate Decay）：

多种学习率衰减方式： $\beta>0$ ，设共经过 $T$ 次迭代，当第 $t$ 次迭代时

分段常数衰减： $\alpha_t=\alpha_0\beta$
逆时衰减： $\alpha_t=\alpha_0 \frac{1}{1+\beta \times t}$
指数衰减： $\alpha_t=\alpha_0 \beta^t \quad \beta<1$
自然指数衰减： $\alpha_t=\alpha_0 e^{-\beta t}$
余弦衰减： $\quad \alpha_t=\frac{1}{2} \alpha_0\left(1+\cos \left(\frac{t \pi}{T}\right)\right)$

学习率预热

==当 $\text {batch size}$ 较大，需要较大的学习率，由于参数是随机初始化的，梯度往往较大，较大的学习率会使训练不稳定。==

学习率预热（Learning Rate Warmup）：为提高训练稳定性，可以在最初几轮迭代时采用较小的学习率，等梯度下降到一定程度后再恢复到初始学习率。

逐渐预热（Gradual Warmup）：设预热阶段共经过 $T^{\prime}$ 次迭代，当第 $t^{\prime}$ 次迭代时迭代次数为

\alpha_t=\frac{t^{\prime}}{T^{\prime}} \alpha_0, \quad 1 \leq t^{\prime} \leq T^{\prime}

预热结束后，再选择一种学习率衰减方法来逐渐降低学习率。

周期性学习率

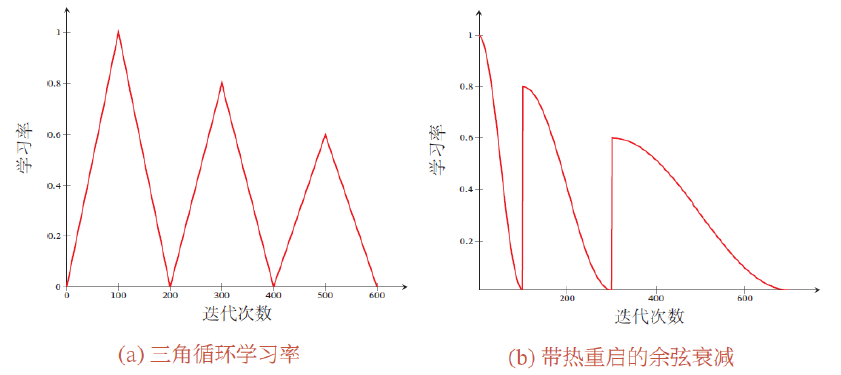
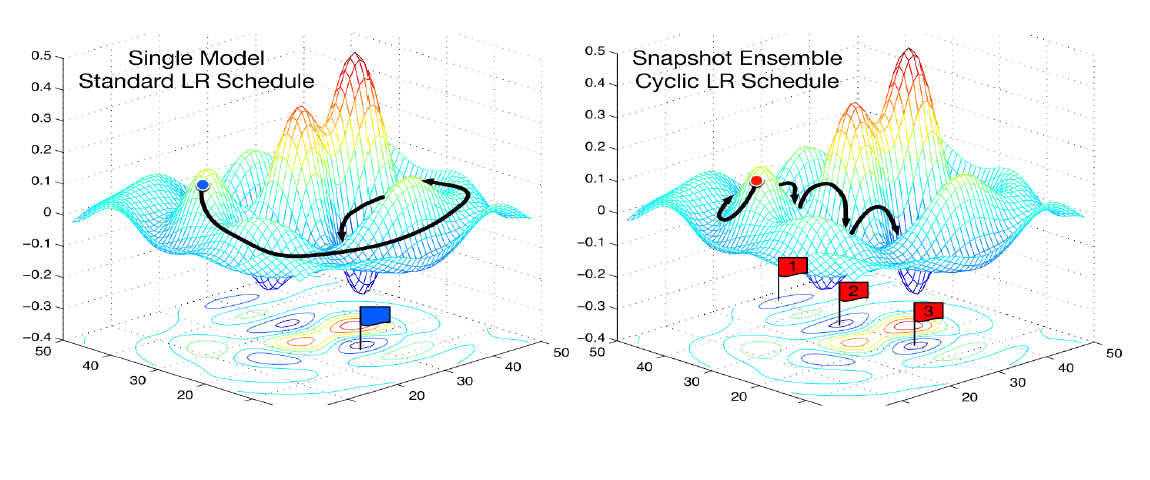
==为了逃离局部最小值或鞍点，可在训练过程中周期性地增大学习率。短期内有损收敛稳定性，长期来看有助于找到更好的局部最优解。==

循环学习率（Cyclic Learning Rate）：让学习率在一个区间内周期性地增大和缩小。

三角循环学习率（Triangular Cyclic Learning Rate）：使用线性缩放来调整学习率。
带热重启的随机梯度下降（Stochastic Gradient Descent with Warm Restarts）：周期性地重启并采用余弦衰减。

自适应学习率

学习率衰减的局限性：

非自适应，不能够根据当前梯度情况做出调整
每个参数的维度上收敛速度都不相同，应该根据不同参数的收敛情况分别设置学习率

AdaGrad 算法

第 $t$ 次迭代，计算每个参数梯度平方的累计值： $G_t=\sum_{\tau=1}^t \mathbf{g}_\tau \odot \mathbf{g}_\tau$
参数更新差值： $\Delta \theta_t=-\frac{\alpha}{\sqrt{G_t+\epsilon}} \odot g_t$

举例： $w_i$ 是模型的一个参数

\theta=\left\{W_1, \ldots, W_i, \ldots, W_{|\theta|}\right\}

\begin{array}{ll} w_i^1 \leftarrow w_i^0-\frac{\alpha}{\sigma_i^0} g_i^0 & \sigma_i^0=\sqrt{\left(g_i^0\right)^2+\epsilon} \\ w_i^2 \leftarrow w_i^1-\frac{\alpha}{\sigma_i^1} g_i^1 & \sigma_i^1=\sqrt{\left(g_i^0\right)^2+\left(g_i^1\right)^2+\epsilon} \\ w_i^3 \leftarrow w_i^2-\frac{\alpha}{\sigma_i^2} g_i^2 & \sigma_i^2=\sqrt{\left(g_i^0\right)^2+\left(g_i^1\right)^2+\left(g_i^2\right)^2+\epsilon} \\ \vdots & \\ w_i^{t+1} \leftarrow w_i^t-\frac{\alpha}{\sigma_i^t} g_i^t & \sigma_i^t=\sqrt{\sum_{\tau=0}^t\left(g_i^\tau\right)^2+\epsilon} \end{array}

RMSprop 算法

第 $t$ 次迭代，计算每个参数梯度平方的指数衰减移动平均值： $G_t =\beta G_{t-1}+(1-\beta) \boldsymbol{g}_t \odot \boldsymbol{g}_t =(1-\beta) \sum_{\tau=1} \beta^{t-\tau} \mathbf{g}_\tau \odot \boldsymbol{g}_\tau$
参数更新差值： $\Delta \theta_t=-\frac{\alpha}{\sqrt{G_t+\epsilon}} \odot g_t$

举例： $w_i$ 是模型的一个参数

\theta=\left\{W_1, \ldots, W_i, \ldots, W_{|\theta|}\right\}

\begin{aligned} & w_i^1 \leftarrow w_i^0-\frac{a}{\sigma_i^0} g_i^0 \quad \sigma_i^0=\sqrt{\beta\left(\sigma_i^0\right)^2+\epsilon} \\ & w_i^2 \leftarrow w_i^1-\frac{a}{\sigma_i^1} g_i^1 \quad \sigma_i^1=\sqrt{\beta\left(\sigma_i^0\right)^2+(1-\beta)\left(g_i^1\right)^2+\epsilon} \\ & w_i^3 \leftarrow w_i^2-\frac{a}{\sigma_i^2} g_i^2 \quad \sigma_i^2=\sqrt{\beta\left(\sigma_i^1\right)^2+(1-\beta)\left(g_i^2\right)^2+\epsilon} \\ \vdots & \\ & w_i^{t+1} \leftarrow w_i^t-\frac{a}{\sigma_i^t} g_i^t \quad \sigma_i^t=\sqrt{\beta\left(\sigma_i^{t-1}\right)^2+(1-\beta)\left(g_i^t\right)^2+\epsilon} \\ & \end{aligned}

梯度优化

需要进行梯度的修正缓解梯度的随机性：

增加批量大小
进行梯度修正

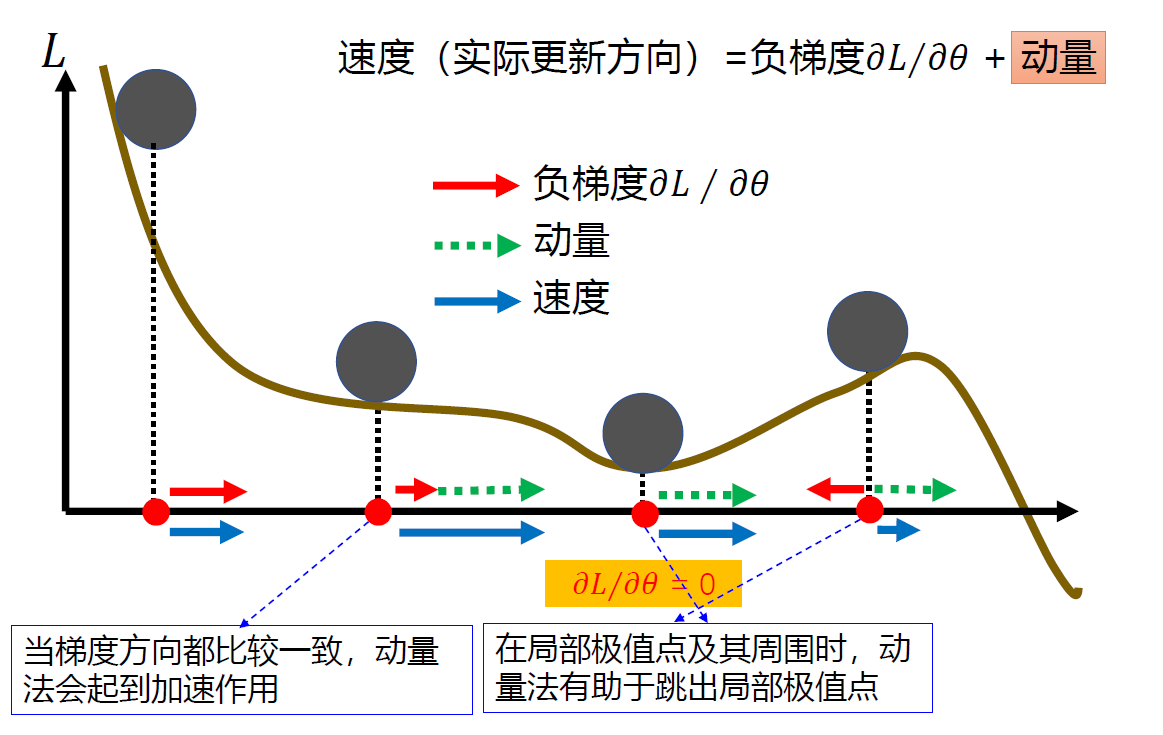
Momentum 算法

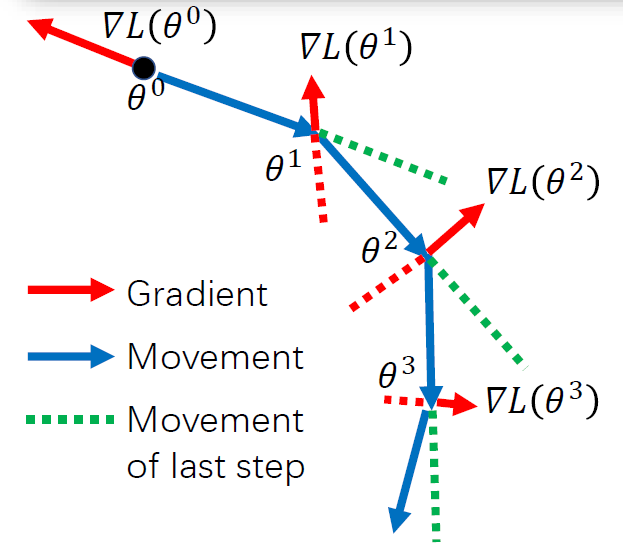
动量法（Momentum）：模拟物理中的概念。一个物体的动量指的是该物体在它运动方向上保持运动的趋势，是该物体的质量和速度的乘积。用之前积累动量来替代真正的梯度，每次迭代的梯度看作是加速度。

v^t=\lambda v^{t-1}-\alpha \mathbf{g}^t \\ \theta^{t+1} \leftarrow \theta^t+v^t

具体过程：

\begin{aligned} & v^0=0 \\ & v^1=-\alpha \mathbf{g}^0 \\ & v^2=-\lambda \alpha \mathbf{g}^0-\alpha \mathbf{g}^1 \\ & v^3=-\lambda^2 \alpha \mathbf{g}^0-\lambda \alpha \mathbf{g}^1-\alpha \mathbf{g}^2 \end{aligned}

每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值。

$\theta^0$ $θ^{0}$
1. 计算梯度： $\nabla L\left(\theta^0\right)$
2. 计算速度更新： $v^0=0$
3. 计算速度更新： $v^1=\lambda v^0-\alpha \nabla L\left(\theta^0\right)=-\alpha \nabla L\left(\theta^0\right)$
$\theta^1=\theta^0+v^1$ $θ^{1} = θ^{0} + v^{1}$
1. 计算梯度： $\nabla L\left(\theta^1\right)$
2. 计算速度更新： $v^2=\lambda v^1-\alpha \nabla L\left(\theta^1\right)=-\lambda \alpha \nabla L\left(\theta^0\right)-\alpha \nabla L\left(\theta^1\right)$
$\theta^2=\theta^1+v^2$ $θ^{2} = θ^{1} + v^{2}$
1. 计算梯度： $\nabla L\left(\theta^2\right)$
2. 计算速度更新： $v^3=\lambda v^2-\alpha \nabla L\left(\theta^2\right)=-\lambda^2 \alpha \nabla L\left(\theta^0\right)-\lambda \alpha \nabla L\left(\theta^1\right)-\alpha \nabla L\left(\theta^2\right)$
$\cdots$

当前时刻的速度不仅依赖于负梯度，还依赖于前序时刻的加权移动平均。

一般而言，在迭代初期，梯度方向都比较一致，动量法会起到加速作用，可以更快地到达最优点。在迭代后期，梯度方向会不一致，在收敛值附近震荡，动量法会起到减速作用，增加稳定性。

Adam 算法

$\text {Adam}$ 算法：自适应学习率（ $\text {RMSprop}$ ）+梯度优化算法（动量法）。

更新有偏一阶矩估计（梯度的指数加权平均）：类似与 $\text {Momentum}$

v^t=\lambda v^{t-1}-\alpha \mathbf{g}^{t-1}

更新有偏二阶矩估计（梯度平方的指数加权平均）：类似与 $\text {RMSprop}$

G^t=\beta G^{t-1}-(1-\beta) \mathbf{g}^t \odot \mathbf{g}^t

修正一阶矩的偏差：

\hat{v}^t=\frac{v^t}{1-\gamma_1^t}

修正二阶矩的偏差：

\hat{G}_t=\frac{G_t}{1-\beta_2^t}

更新参数：

\theta^t=\theta^{t-1}-\frac{\alpha}{\sqrt{\hat{G}^t+\delta}} \hat{v}^t

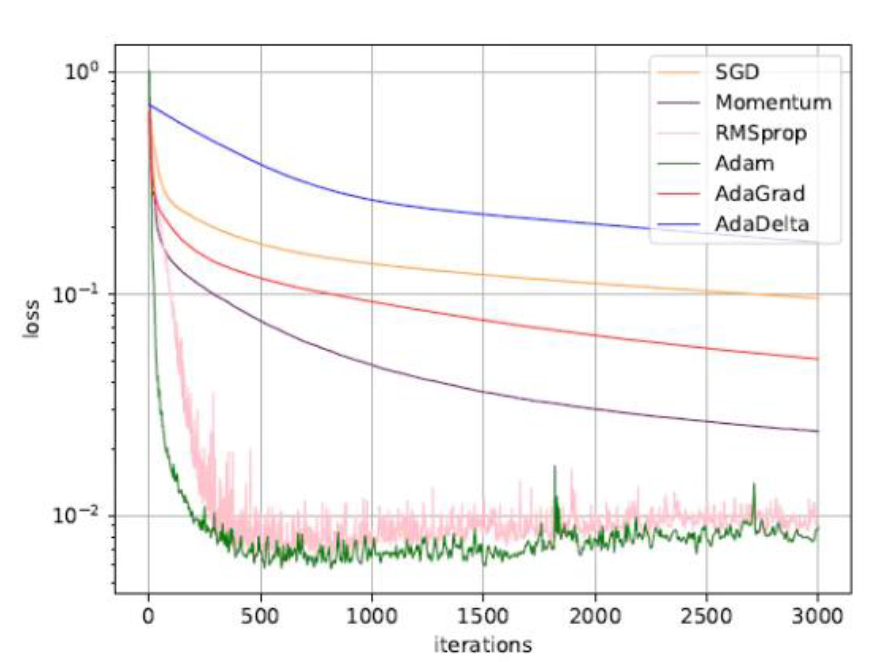
各种优化算法比较（数据集上收敛性的比较（学习率为 0.001 ，批量大小为 128）

梯度截断

除了梯度消失之外，梯度爆炸也是影响学习效率的主要因素。为了避免这种情况，当梯度的模大于一定阈值时，就对梯度进行截断，称为梯度截断（ $\text {Gradient Clipping}$ ）。

按值截断：

\mathbf{g}_t=\max \left(\min \left(\boldsymbol{g}_t, b\right), a\right)

按模阶段：如果 $\left\|\boldsymbol{g}_t\right\|^2 \leq b$ ，保持 $\boldsymbol{g}_t$ 不变. 如果 $\left\|\boldsymbol{g}_t\right\|^2>b$ ，令

\mathbf{g}_t=\frac{b}{\left\|\boldsymbol{g}_t\right\|} \mathbf{g}_t

学习率与梯度优化小结

解决问题：帮助网络快速平稳收敛——逃离局部极值点、鞍点、抑制梯度爆炸。

学习率调整
- 学习率衰减
- 学习率预热
- 自适应算法： $\text {AdaGrad}$ 算法/ $\text {RMSprop}$ 算法/ $\text {Adam}$ 算法
- 周期性学习率
梯度修正
- 动量法
- 梯度截断

参数初始化与数据预处理

参数初始化

基于固定方差的参数初始化

高斯分布初始化：从一个固定均值和方差的高斯分布进行随机初始化。

均匀分布初始化：在一个区间 $[-r.r]$ 内采用均匀分布进行初始化。

一般而言，参数初始化的区间应该根据神经元的性质进行差异化的设置：一个神经元的输入连接很多，它的每个输入连接上的权重应该小一点避免神经元的输出过大（ $\text {eg.ReLU}$ ）或过饱和（ $\text {eg.sigmoid}$ ）。

初始化一个深度网络时，为了缓解梯度消失或者爆照问题，须尽可能保持每个神经元的输入和输出的期望始终为 $0$ ，方差保持一致：根据神经元的连接数量自适应地调整初始化分布的方差。

方差缩放的目标：

E\left[a^{[l-1]}\right]=E\left[a^{[l]}\right]=0 \quad \operatorname{Var}\left[a^{[l-1]}\right]=\operatorname{Var}\left[a^{[l]}\right]

基于方差缩放的参数初始化：Xavier 初始化

假设一个神经网络中，第 $l$ 层的一个神经元输出为 $a^{(l)}$ ，与前一层 $M_{l-1}$ 个神经元相连：

a^{(l)}=f\left(\sum_{i=1}^{M_{l-1}} w_i^{(l)} a_i^{(l-1)}\right)

简化问题，激活函数为恒等函数 $f(x)=x$

假设，前一层的输出 $a_i^{(l-1)}$ 和本层的参数 $w_i^{(l)}$ 的均值都为 $0$ ，且互相独立，则 $a^{(l)}$ 的均值和方差分别为：

\begin{aligned} \mathbb{E}\left[a^{(l)}\right] & =\mathbb{E}\left[\sum_{i=1}^{M_{l-1}} w_i^{(l)} a_i^{(l-1)}\right]=\sum_{i=1}^{M_{l-1}} \mathbb{E}\left[w_i^{(l)}\right] \mathbb{E}\left[a_i^{(l-1)}\right]=0 . \end{aligned}

\begin{aligned} \operatorname{var}\left(a^{(l)}\right) & =\operatorname{var}\left(\sum_{i=1}^{M_{l-1}} w_i^{(l)} a_i^{(l-1)}\right)=\sum_{i=1}^{M_{l-1}} \operatorname{var}\left(w_i^{(l)}\right) \operatorname{var}\left(a_i^{(l-1)}\right)=M_{l-1} \operatorname{var}\left(w_i^{(l)}\right) \operatorname{var}\left(a_i^{(l-1)}\right) . \end{aligned}

也就是要有 $M_{l-1} \operatorname{var}\left(w_i^{(l)}\right)=1$ ，即

\begin{aligned} \operatorname{var}\left(w_i^{(l)}\right)=\frac{1}{M_{l-1}} \end{aligned}

又

\begin{aligned} \operatorname{var}\left(w_i^{(l)}\right)=\frac{1}{M_l} \end{aligned}

故

\operatorname{var}\left(w_i^{(l)}\right)=\frac{2}{M_{l-1}+M_l}

计算出参数的理想方差后，可以通过高斯分布或者均匀分布来随机初始化参数：

高斯分布： $\mathcal{N}\left(0, \frac{2}{M_{l-1}+M_l}\right)$
均匀分布： $r=\sqrt{\frac{6}{M_{l-1}+M_l}}$

虽然在 $\text Xavier$ 初始化中我们假设激活函数为恒等函数，但是 $\text Xavier$ 初始化也适用于 $\text Logistic$ 函数和 $\text Tanh$ 函数（神经元参数和输入都比较小，处于激活函数的线性区间）。

$\text Logistic$ 函数斜率约为 $\frac{1}{4}$ ，因此 $f(x)=\frac{1}{4} x$

\operatorname{var}\left(w_i^{(l)}\right)=16 \times \frac{2}{M_{l-1}+M_l}

He 初始化

当第 $l$ 层神经元使用 $\text {ReLU}$ 激活函数时，通常有一半的神经元输出为 $\text {0}$ ，因此其分布的方差也近似为使用恒等函数时的一半。这样，只考虑前向传播时，参数 $w_i^{(l)}$ 的理想方差为：

\operatorname{var}\left(w_i^{(l)}\right)=\frac{2}{M_{l-1}}

计算出参数的理想方差后，可以通过高斯分布或者均匀分布来随机初始化参数：

高斯分布： $\mathcal{N}\left(0, \frac{2}{M_{l-1}}\right)$
均匀分布： $r=\sqrt{\frac{6}{M_{l-1}}}$

初始化方法	激活函数	均匀分布	高斯分布
$\text Xavier$ 初始化	$\text Logistic$	$r=4 \sqrt{\frac{6}{M_{l-1}+M_l}}$	$\sigma^2=16 \times \frac{2}{M_{l-1}+M_l}$
$\text Xavier$ 初始化	$\text Tanh$	$r=\sqrt{\frac{6}{M_{l-1}+M_l}}$	$\sigma^2=\frac{2}{M_{l-1}+M_l}$
$\text {He}$ 初始化	$\text {ReLU}$	$r=\sqrt{\frac{6}{M_{l-1}}}$	$\sigma^2=\frac{2}{M_{l-1}}$

正交初始化

用均值为 $0$ 、方差为 $1$ 的高斯分布初始化一个矩阵，将这个矩阵用奇异值分解得到两个正交矩阵，并使用其中之一作为权重矩阵。

数据预处理

数据归一化

简单缩放：最小最大值归一化；图像像素值除以 $255$

x_i \leftarrow \frac{x_i-\min \left(x_i\right)}{\max \left(x_i\right)-\min \left(x_i\right)}

逐样本均值消减/移除直流分量
特征标准化：使得数据的每一个维度具有零均值和单位方差。

x_i \leftarrow \frac{x_i-u_i}{\sigma_i}

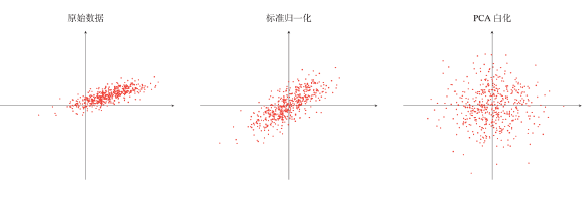
白化

降低输入的冗余性，降低特征之间的相关性，使得所有的特征具有相同的方差。

$\text {PCA}$ 白化：先 $\text {PCA}$ 进行基转换，降低数据的相关性，再对每个输入特征进行缩放(除以各自的特征值的开方)，以获得单位方差，此时的协方差矩阵为单位矩阵。
$\text {ZCA}$ 白化： $\text {ZCA}$ 白化只是在 $\text {PCA}$ 白化的基础上做了一个逆映射操作，使数据转换到原始基下，使得白化之后的数据更加的接近原始数据。

实际建议

样例	归一化	白化
自然灰度图像	均值消减	$\text {PCA/ZCA}$ 白化
彩色图像	简单缩放	$\text {PCA/ZCA}$ 白化
音频（ $\text {MFCC}$ /频谱图）	特征均值化	$\text {PCA/ZCA}$ 白化
$\text {MNIST}$ 手写数字	简单缩放/均值消减	$\text {PCA/ZCA}$ 白化

输入数据归一化了，中间输出数据如何？

逐层归一化

目的：解决内部协变量偏移问题；解决梯度消失、梯度爆炸；获得更平滑的优化地形。

归一化方法：

批量归一化
层归一化
权重归一化

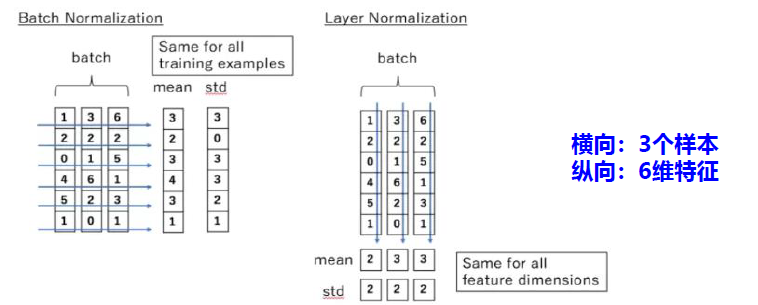
批量归一化

批量归一化是对一个中间层的单个神经元进行归一化操作。

第 $l$ 层，对于 $K$ 个样本的一个小批量集合 $Z^{(l)}=\left[\mathbf{z}^{(1, l)}, \ldots, \mathbf{z}^{(K, l)}\right]$ ，其均值方差为：

u_{\mathrm{B}}=\frac{1}{K} \sum_{k=1}^K \mathbf{z}^{(k, l)} \quad \sigma_B^2=\frac{1}{K} \sum_{k=1}^K\left(\mathbf{z}^{(k, l)}-u_{\mathrm{B}}\right) \odot\left(\mathbf{z}^{(k, l)}-u_{\mathrm{B}}\right)

\hat{\mathbf{Z}}^{(l)}=\frac{\mathbf{Z}^{(l)}-u_{\mathrm{B}}}{\sqrt{\sigma_B^2+\varepsilon}} \bar{\rho}+\beta \triangleq B N_{\gamma, \beta}\left(\mathbf{Z}^{(l)}\right)

针对 $K$ 个样本进行归一化

层归一化

层归一化是对一个中间层的所有神经元进行归一化。

第 $l$ 层，对于所有的样本集合 $Z^{(k)}=\left[\mathbf{z}^{(k, 1)}, \ldots, \mathbf{z}^{(k, L)}\right]^T$ ，其均值方差为：

u_L=\frac{1}{L} \sum_{l=1}^{L} \mathbf{z}^{(k, l)} \quad \sigma_B^2=\frac{1}{L} \sum_{l=1}^L\left(\mathbf{z}^{(k, l)}-u_{\mathrm{L}}\right) \odot\left(\mathbf{z}^{(k, l)}-u_{\mathrm{L}}\right)

\hat{\mathbf{Z}}^{(l)}=\frac{\mathbf{Z}^{(l)}-u^{(l)}}{\sqrt{\sigma^{(l)^2}+\varepsilon}} \odot \gamma+\beta \triangleq L N_{\gamma, \beta}\left(\mathbf{Z}^{(l)}\right)

针对 $n$ 个神经元进行归一化

批量归一化 VS 层归一化

批量归一化：对每一行进行归一化，不同样本同一特征。

层归一化：对每一列进行归一化，不同特征同一样本。

一般选择批量归一化，当样本数量较小时，选择层归一化。

超参数优化

神经网络中的超参数：

层数
每层神经元个数
激活函数
学习率（各优化算法中包含的参数）
正则化系数
$\text {mini-batch}$ 大小

网格搜索

网格搜索：通过尝试所有超参数的组合来寻址合适的一组超参数配置的方法。

假设一共有 $K$ ，第 $k$ 个超参数可以取 $m_k$ 个值，一共有

m_1 \times m_2 \times \cdots \times m_K

个取值组合。

随机搜索

随机搜索：对超参数进行随机组合，选取一个性能最好的配置。

贝叶斯优化

贝叶斯优化：自适应的超参数优化方法，根据当前已经试验的超参数组合，来预测下一个可能带来最大收益的组合。

假设超参数的优化函数 $f(x)$ 服从高斯分布，则 $p(f(x) \mid x)$ 为一个正态分布

贝叶斯优化根据已有的 $N$ 组试验结果 $H=\left\{x_n, y_n\right\}_{n=1}^N$ （ $y_n$ 为 $f(x_n)$ 的观测值）来建模高斯过程，并计算 $f(x)$ 的后验分布 $p G P(f(x) \mid x, H)$ 。

需用尽可能少的样本使得后验分布接近真实分布，定义一个收益函数 $\mathrm{a}(x, H)$ 收益函数来判断一个样本是否能够给建模后验概率提供更多的收益，收益函数的定义有很多种方式，一个常用的是期望改善。

动态资源分配

过拟合与正则化

如何提高神经网络的泛化能力？

$\ell_1$ 和 $\ell_2$ 正则化
提前停止
$\text Dropout$
数据增强

$\ell_1$ 和 $\ell_2$ 正则化

$\ell_1$ 和 $\ell_2$ 正则化：最常用的正则化方法，通过约束参数的 $\ell_1$ 和 $\ell_2$ 范数来减小模型在训练数据集上的过拟合现象。

\mathrm{L}_{\circ}^{\prime}(\theta)=L(\theta)+\lambda \ell_p(\theta)

$\ell_1$ 正则化： $\mathrm{L}^{\prime}(\theta)=L(\theta)+\lambda \frac{1}{2}\|\theta\|_2 \quad \frac{\partial \mathrm{L}^{\prime}}{\partial \theta}=\frac{\partial \mathrm{L}}{\partial \theta}+\lambda \theta$

\theta^{t+1} \rightarrow \theta^t-\alpha \frac{\partial \mathrm{L}^{\prime}}{\partial \theta}=\theta^t-\alpha\left(\frac{\partial \mathrm{L}}{\partial \theta}+\lambda \theta^t\right)=(1-\alpha \lambda) \theta^t-\alpha \frac{\partial \mathrm{L}}{\partial \theta}

$\ell_2$ 正则化： $\mathrm{L}^{\prime}(\theta)=L(\theta)+\lambda \frac{1}{2}\|\theta\|_1 \quad \frac{\partial \mathrm{L}^{\prime}}{\partial \theta}=\frac{\partial \mathrm{L}}{\partial \theta}+\lambda \operatorname{sgn}(\theta)$

\theta^{t+1} \rightarrow \theta^t-\alpha \frac{\partial \mathrm{L}^{\prime}}{\partial \theta}=\theta^t-\alpha\left(\frac{\partial \mathrm{L}}{\partial \theta}+\lambda \operatorname{sgn}\left(\theta^t\right)\right)=\theta^t-\alpha \frac{\partial \mathrm{L}}{\partial \theta}-\alpha \lambda \operatorname{sgn}\left(\theta^t\right)

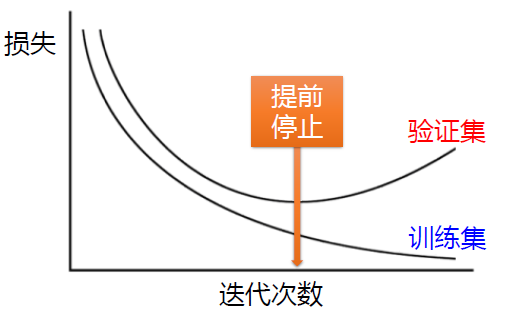
提前停止

使用一个验证集来测试每一次迭代的参数在验证集上是否最优。如果在验证集上的错误率不再下降，就停止迭代。

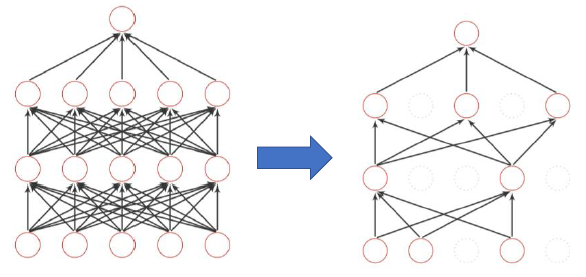
$\text Dropout$

训练：在每次更新参数前：每个神经元以 $p \%$ 的概率被丟弃（网络结构发生了改变）

测试：不用 $\text dropout$ ，每个参数乘以 $1-p \%$