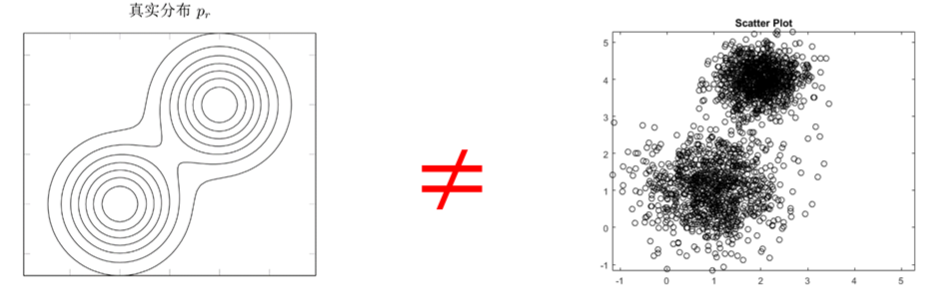机器学习基本概念
机器学习 ≈ 构建一个映射函数
机器学习三要素:模型、学习准则、优化算法
以线性回归(Linear Regression)为例:
期望风险(Expected Risk):对所有样本(未知样本+已知训练样本)的预测能力。【全局】
R(θ)=E(x,y)∼pr(x,y)[L(y,f(x;θ))]
经验风险(Empirical Risk):对所有已知训练样本都求损失函数,再累加求平均,表示决策函数对已知训练样本的预测能力。【局部】
D={x(n),y(n)},n∈[1,N]
RDemp(θ)=N1n=1∑NL(y,f(x;θ))
期望最小化风险,是指真实数据分布和映射函数未知情况下,通过参数寻找使得期望风险最小化。首先期望风险不可计算,常用经验风险来近似。然后寻找一组最优的参数 θ∗,使经验风险函数最小化。
机器学习求解问题 ⇒ 最优化问题
优化目标:经验风险最小化 RDemp(θ)=N1∑n=1NL(y,f(x;θ))
优化输出:寻找一组最优的参数 θ∗
损失函数(Loss Function):
L(y,f(x;θ))
定义损失函数的一般方法:
| 损失函数 |
表达式 |
| 0−1 损失函数 |
L(y,f(x;θ))={01 if y=f(x;θ) if y=f(x;θ)=I(y=f(x;θ)) |
| 平方损失函数 |
L(y,f(x;θ))=21(y−f(x;θ))2 |
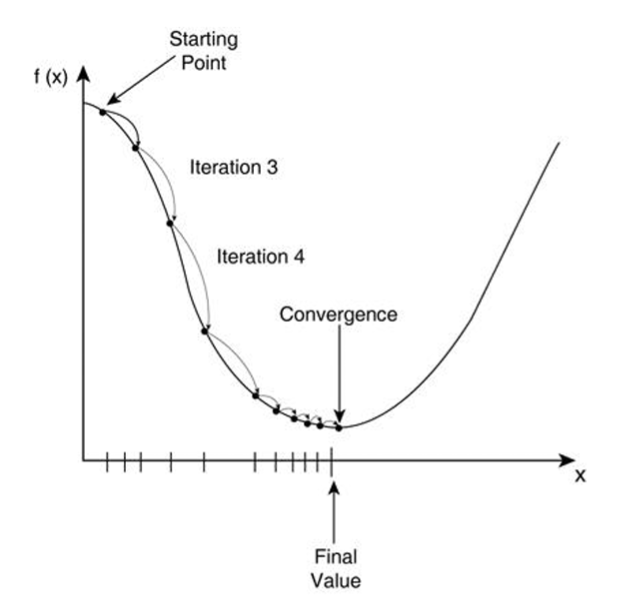
假设一个人需要从山的某处开始下山,尽快到达山底。在下山之前他需要确认两件事:下山的方向和下山的距离。因为下山的路有很多,他必须利用一些信息,找到从该处开始最陡峭的方向下山,这样可以保证他尽快到达山底。此外,这座山最陡峭的方向并不是一成不变的,每当走过一段规定的距离,他必须停下来,重新利用现有信息找到新的最陡峭的方向。通过反复进行该过程,最终抵达山底。
| 下山 |
无约束优化 |
| 山 |
优化函数表达式 |
| 山底 |
函数最优值 |
| 下山的距离 |
学习率 |
| 下山的方向 |
梯度方向 |
| 某处 |
优化函数初始值 |
批量梯度下降(Gradient Descent):
- 给定待优化连续可微函数 J(Θ) 、学习率 α 以及一组初始值 Θ0=(θ01,θ02,⋯,θ0l,)
- 计算待优化函数梯度: ∇J(Θ0)
- 更新迭代公式: Θ0+1=Θ0−α∇J(Θ0)
- 计算 Θ0+1 处函数梯度 ∇J(Θ0+1)
- 计算梯度向量的模来判断算法是否收敛: ∥∇J(Θ)∥⩽ε
- 若收敛,算法停止,否则根据迭代公式继续迭代
推广到学习准则中的经验风险,经过迭代计算风险函数的最小值:
RDemp(θ)=N1n=1∑NL(y,f(x;θ))θt+1=θt−α∂θ∂RDemp(θ)=θt−αN1n=1∑N∂θ∂L(y(n),f(x(n);θ))
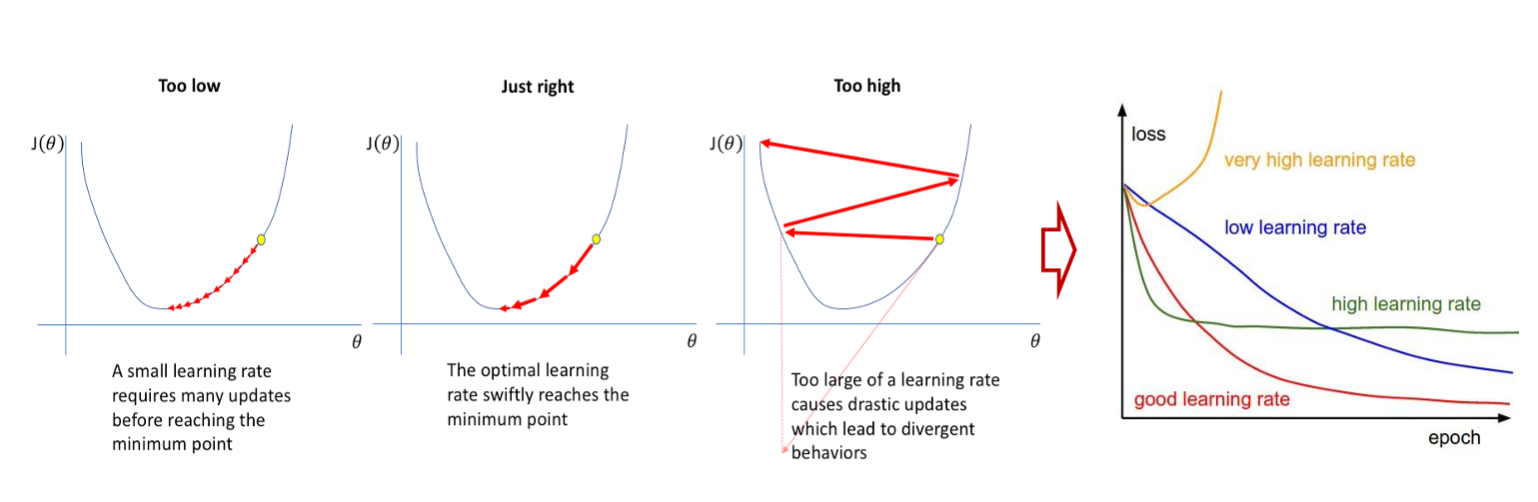
学习率是十分重要的!
- 学习率超大,无法收敛
- 学习率过大,无法收敛到合理区间
- 学习率过小,收敛速度慢
随机梯度下降法(Stochastic Gradient Descent,SGD):批量梯度下降法在每次迭代都需计算每个训练样本上损失函数的梯度并加和,计算复杂度较大;为了降低迭代的计算复杂度,可以每次迭代只采集一个训练样本,计算该样本的损失函数的梯度并更新参数,即随机梯度下降法。
小批量(Mini-Batch )随机梯度下降法:批量梯度下降和随机梯度下降的折中。每次迭代时,随机选取一小部分训练样本来计算梯度并更新参数,这样既可以兼顾随机梯度下降法的优点,也可以提高训练效率。
提前停止法:验证集错误率不再下降,就停止迭代。
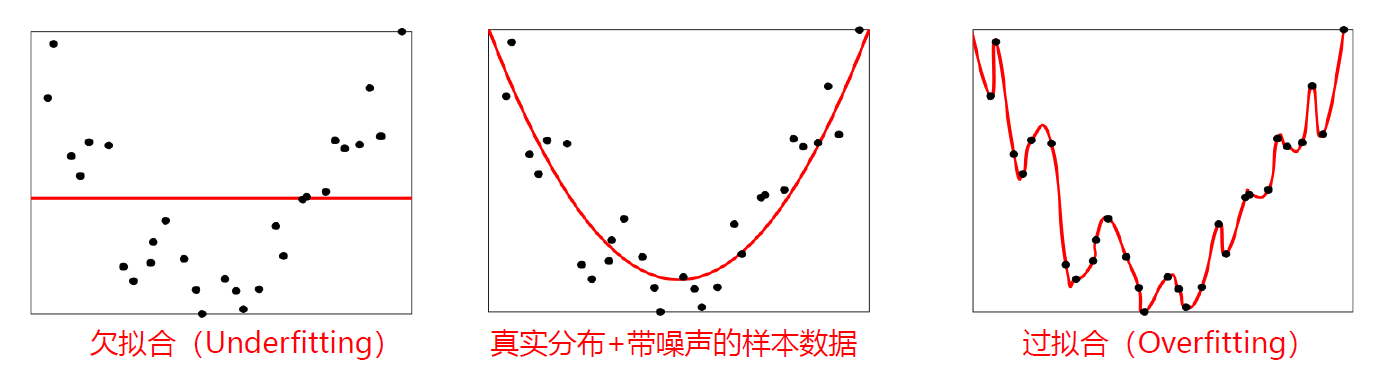
欠拟合(Underfitting)和欠拟合(Overfitting)
欠拟合:模型不能很好地拟合训练数据,在训练集的错误率高;模型能力不足,不能掌握训练样本的一般性质。
过拟合:训练数据少 or 模型能力强,将训练集的本身特点当做所有样本的一般性质,导致泛化性能下降。
根据前面提到的:
| 期望风险 |
经验风险 |
| R(θ)=E(x,y)∼pr(x,y)[L(y,f(x;θ))] |
RDemp(θ)=N1∑n=1NL(y,f(x;θ)) |
泛化错误:可以衡量一个机器学习模型是否可以很好地泛化到未知数据,一般表现在一个模型在训练集和测试集上的错误率。
GD(f)=R(f)−RDemp(f)
正则化(Regularization):通过限制模型复杂度,从而避免过拟合,提高泛化能力的方法。
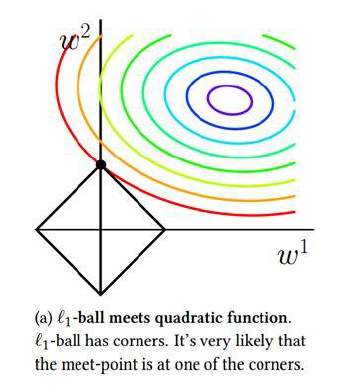
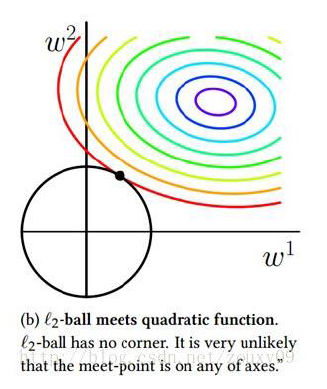
l1 和 l2 正则化:
θ∗=θargminN1n=1∑NL(y(n),f(x(n);θ))+ℓp(θ)
| L1 正则项 |
L2 正则项 |
| ∥w∥1 |
∥w∥22 |
 |
 |
数学基础
线性代数
基本概念:
- 标量(scalar):一个单独的数。
- 向量(vector):一列数。
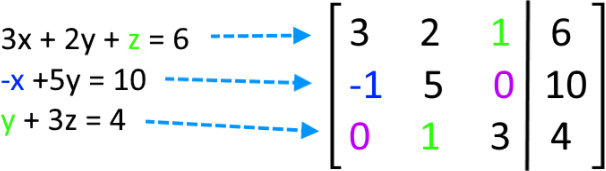
- 矩阵(matrix):二维数组。
- 张量(tensor):超过二维的数组。
矩阵运算:
范数:
- l1 范数:向量的各个元素的绝对值之和。
- ∥v∥1=∑n=1N∣vn∣
- l2 范数:向量的各个元素的平方和再开平方。
- ∥v∥2=∑n=1Nvn2=v⊤v
- ℓ∞ 范数:向量的各个元素的最大绝对值。
- ∥v∥∞=max{v1,v2,⋯,vN}
矩阵的范数,常用 lp 范数一般定义:
∥A∥p=(m=1∑Mn=1∑N∣amn∣p)1/p
矩阵的 F 范数是向量的 l2 范数的推广:∥W∥F=∑m=1M∑n=1N(wmn)2。
微积分基础
导数:曲线的斜率,反应曲线变化的快慢。
f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)
高阶导数:函数的更高阶求导。
偏导数::多元函数在保持其他变量固定,关于其中一个变量的求导。
方向导数:函数对某一方向求导。
常见函数的导数:
| 函数 |
函数形式 |
导数 |
| 常函数 |
f(x)=C, 其中 C 为常数 |
f′(x)=0 |
| 幂函数 |
f(x)=xr, 其中 r 是非零实数 |
f′(x)=rxr−1 |
| 指数函数 |
f(x)=exp(x) |
f′(x)=exp(x) |
| 对数函数 |
f(x)=log(x) |
f′(x)=x1 |
泰勒公式:函数 f(x) 以已知某一点的各阶导数值的作系数构建一个多项式来近似函数在某一点的邻域的值。
f(x)=f(a)+1!1f′(a)(x−a)+2!1f(2)(a)(x−a)2+⋯+n!1f(n)(a)(x−a)n+Rn(x)
Rn(x):泰勒公式的余项,(x−a)n 的高阶无穷小。
方向导数与梯度:梯度向量是方向导数最大的方向。
矩阵微分:多元微积分的一种表达方式,即使用矩阵和向量来表示因变量每个成分关于自变量每个成分的偏导数。
分为
矩阵:A ,其元素记作 aij ;
向量:x,其元素记作 xi
标量:t、α
矩阵、向量对标量求导:结果与矩阵、向量同型,每个元素就是矩阵、向量相应分量对标量的求导。
-
F:R→Rm×n,∂F/∂x 是 m×n 维矩阵,(∂F/∂x)ij=∂fij/∂x
-
或者记作 ∇xF 或 Fx′
-
f:R→Rm,∂f/∂x 是 m 维向量,(∂f/∂x)i=∂fi/∂x
- 行向量 fT 记作∇xfT 或 ∂fT/∂x
- 列向量 f 记作 ∇xf 或 ∂f/∂x
标量对矩阵、向量求导:结果与矩阵、向量同型,每个元素就是标量对矩阵、向量相应分量的求导。
-
f:Rm×n→R,∂f/∂X 是 m×n 维矩阵,(∂f/∂X)ij=∂f/∂xij
-
f:Rm→R,∂f/∂x 是 m 维向量,(∂f/∂x)i=∂f/∂xi
- 行向量 fT 记作∇xTf 或 ∂f/∂xT
- 列向量 f 记作 ∇xf 或 ∂f/∂x
向量对向量求导:雅可比矩阵
- f:Rn→Rm, ∂f/∂x 是 m×n 维矩阵,(∂f/∂x)ij=∂fi/∂xj
- 或者记作 ∇xf∘
举例常见:
- 标量 (y∈R) 关于向量 (x∈RM) 的偏导数
- ∂x∂y=[∂x1∂y,⋯,∂xM∂y]⊤∈RM×1
- 向量 (y∈RN) 关于标量 (x∈R) 的偏导数
- ∂x∂y=[∂x∂y1,⋯,∂x∂yN]∈R1×N
- 向量 (y=f(x)∈RN) 关于向量 (x∈RM) 的偏导数
- ∂x∂f(x)=⎣⎢⎢⎡∂x1∂y1⋮∂xM∂y1⋯⋱⋯∂x1∂yN⋮∂xM∂yN⎦⎥⎥⎤∈RM×N
微分链式法则:
- 标量微分链式法则:若 x∈R,y=g(x)∈R,z=f(y)∈R,
- dxdz=dxdydydz
- 向量微分链式法则:
- 若 x∈R,y=g(x)∈RM,z=f(y)∈RN,(标量 → 向量 → 向量)
- ∂x∂z=∂x∂y∂y∂z∈R1×MRM×N=R1×N
- 若 x∈RM,y=g(x)∈RN,z=f(y)∈RK ,(向量 → 向量 → 向量)
- ∂x∂z=∂x∂y∂y∂z∈RM×NRN×K=RM×K
- 若 X∈RM×N,y=g(X)∈RN,z=f(y)∈R ,(矩阵 → 向量 → 标量)
- ∂xij∂z=∂xij∂y∂y∂z∈R1×NRN×1=R
概率与统计基础
条件概率:p(y∣x)≜P(Y=y∣X=x)=p(x)p(x,y)
贝叶斯公式:p(y∣x)=p(x)p(x∣y)p(y)
常见概率分布:
- 离散随机变量的概率分布:伯努利分布、二项分布
- 连续随机变量概率分布:均匀分布、正态分布
…
常用模型
线性回归
线性模型(Linear Model):机器学习中应用最广泛的模型,指通过样本特征的线性组合来进行预测的模型。
给定一个 D 维样本 x=[x1,⋯,xD]T,其线性组合函数:
f(x;w,b)=w1x1+w2x2+⋯+wDxD+b=w⊤x+b
线性回归是一种典型的线性模型:输出的标签是连续值;
分类问题:输出的标签是离散值。
引入函数 g(⋅) ,使输出符合预期离散值得目标。
y=g(f(x;w,b))
f(x;w,b):线性判别函数(Discriminant Function)
g(⋅):非线性决策函数(Decision Function)
举例:g(⋅) 可以是符号函数(Sign Function)
g(f(x;w,b))=sgn(f(x;w,b))≜{+1−1 if if f(x;w,b)>0,f(x;w,b)<0.
Logistic 回归
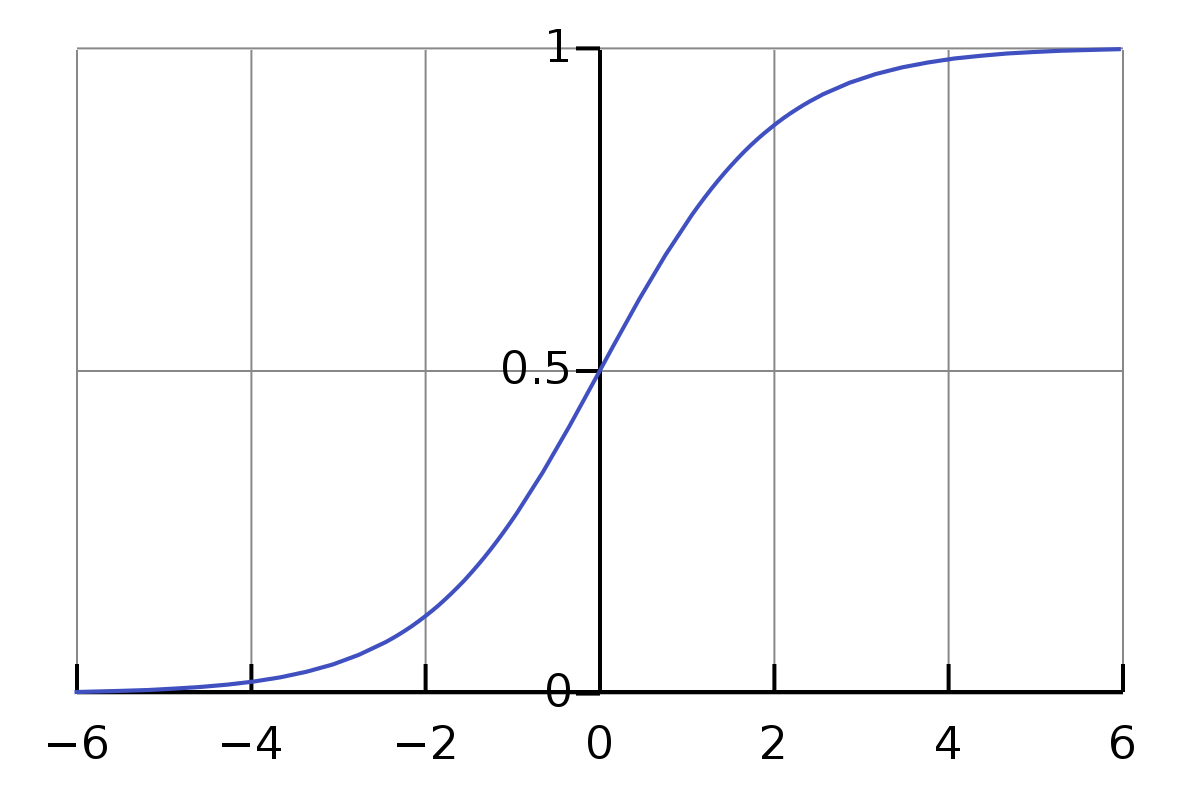
g(⋅) 选择为 Logistic 函数
σ(x)=1+exp(−x)1
- 模型:分类决策问题 → 条件概率估计问题。
- 线性函数组合特征:f=w⊤x+b
- 非线性函数决策:
p(y=1∣x)=σ(w⊤x)≜1+exp(−w⊤x)1p(y=0∣x)=1−p(y=1∣x)=1+exp(−w⊤x)exp(−w⊤x)
模型预测条件概率:
pω(y=1∣x)=σ(ωTx+b);pω(y=0∣x)=1−σ(ωTx+b)
真实条件概率:
pr(y=1∣x)=y∗;pr(y=0∣x)=1−y∗
熵(Entropy):信息论中,用来衡量一个随机事件的不确定性。表示为自信息的期望。
自信息(Self Information):I(x)=−log(p(x))
H(X)=EX[I(x)]=EX[−logp(x)]=−x∈X∑p(x)logp(x)
交叉熵(Cross Entropy):按照概率分布 q 的最优编码对真实分布为 p 的信息进行编码的长度。
H(p,q)=Ep[−logq(x)]=−x∑p(x)logq(x)
在给定 p 的情况下, 如果 p 和 q 越接近,交叉熵越小 。如果 p 和 q 差别越大,交叉熵就越大。
给定 N 个训练样本 {(x(n),y(n))}n=1N,使用 Logistic 回归模型进行预测,单个样本预测概率:
y^(n)=σ(w⊤x(n)),1≤n≤N
又训练样本 {(x(n),y(n))}n=1N,单个样本真实概率:
pr(y(n)=1∣x(n))=y(n),pr(y(n)=0∣x(n))=1−y(n)
真实概率和预测概率的交叉熵为:−[pr(y(n)=1∣x(n))logy^(n)+pr(y(n)=0∣x(n))log(1−y^(n))]
考虑全部训练样本,基于交叉熵损失函数,模型在训练集上的风险函数为:
R(w)=−N1n=1∑N(pr(y(n)=1∣x(n))logy^(n)+pr(y(n)=0∣x(n))log(1−y^(n)))=−N1n=1∑N(y(n)logy^(n)+(1−y(n))log(1−y^(n)))
- 优化算法:使用梯度下降,针对的是 w,上述与该项有关系的只有 y^(n)。
∂w∂R(w)=−N1n=1∑N(y(n)y^(n)y^(n)(1−y^(n))x(n)−(1−y(n))1−y^(n)y^(n)(1−y^(n))x(n))=−N1n=1∑N(y(n)(1−y^(n))x(n)−(1−y(n))y^(n)x(n))=−N1n=1∑Nx(n)(y(n)−y^(n))
wt+1←wt+αN1n=1∑Nx(n)(y(n)−y^wt(n))
| 要素 |
公式 |
| 模型 |
p(y=1∣x)=σ(wTx)≜1+exp(−wTx)1 |
| 学习准则 |
R(w)=−N1∑n=1N(y(n)logy^(n)+(1−y(n))log(1−y^(n))) |
| 优化算法 |
∂w∂R(w)=−N1∑n=1Nx(n)(y(n)−y^(n))wt+1←wt+αN1∑n=1Nx(n)(y(n)−y^wt(n)) |
Softmax 回归
多分类问题(Multi class Classification):分类的类别数大于 2。分类一般需要多个线性判别函数,但设计这些判别函数有很多种方式。
假设一个多分类问题类别有 {1,2,⋯,C},常用的方式:
- “一对其余”方式:把多分类问题转换为 C 个“一对其余”的二分类问题。这种方式共需要 C 个判别函数,其中第 i 个判别函数 fi 是将类别 i 的样本和不属于类别 i 的样本分开。
- "一对一"方式:把多分类问题转换为 2C(C−1) 个“一对一”的二分类问题。这种方式共需要 2C(C−1) 个判别函数,其中第 (i,j) 个判别函数是把类别 i 和类别 j 的样本分开。
- “argmax”方式:改进的“一对其余”方式。这种方式共需要 C 个判别函数。
对于样本 x ,如果存在一个类别 c ,相对于所有的其他类别 c~(c~=c) 有 fc(x;wc,b)>fc~(x,wc~,b) ,那 么 x 属于类别 c0。
y=c=1CCmaxfc(x;wc,b)
多类线性可分:对于训练集 D={(x(n),y(n))}n=1N,如果存在 C 个 权重向量 w1∗,⋯,wC∗,使得第 c(1≤c≤C) 类的所有样本都满足 fc(x;wc∗,b)> fc~(x,wc~∗,b),∀c~=c, 那么训练集 D 是线性可分的。
从上面定义可知,如果数据集是多类线性可分的,那么一定存在一个“argmax”方式的线性分类器可以将它们正确分开。
Softmax Regression 也称为多项(Multinomial)或多类(Multi Class)的 Logistic 回归,是 Logistic 回归在多分类问题上的推广。
softmax(xk)=∑i=1Kexp(xi)exp(xk)
- 模型:分类决策问题 → 条件概率估计问题
- 线性函数组合特征:f=w⊤x+b
- 非线性函数决策,Softmax 回归:wi 是第 i 类的权重向量
p(y=c∣x)=softmax(wc⊤x+b)=∑c′=1Cexp(wc′⊤x+b)exp(wc⊤x+b)
- 学习准则: Softmax 回归使用交叉熵作为损失函数
给定 N 个训练样本 {(x(n),y(n))}n=1N,使用 Softmax 回归模型进行预测,单个样本预测概率:
y^(n)=c=1argmaxCp(y=c∣x)
又训练样本 {(x(n),y(n))}n=1N,单个样本真实概率:
y(n)
| 种类 |
预测概率 |
真实概率 |
| 1 |
y^1(n) |
y1(n) |
| 2 |
y^2(n) |
y2(n) |
| ⋯ |
|
|
| i |
y^i(n) |
yi(n) |
| ⋯ |
|
|
| C |
y^C(n) |
yC(n) |
考虑全部样本,可以写为:
y^=softmax(W⊤x)=1C⊤exp(W⊤x)exp(W⊤x)
- W=[w1,⋯,wC] :由 C 个类的权重向量组成的矩阵。
- 1C : C 维的全 1 向量。
- y^∈RC :所有类别的预测条件概率组成的向量,第 c 维的值是第 c 类的预测条件概率。
真实概率和预测概率的交叉熵为:−[y1(n)logy^1(n)+y2(n)logy^2(n)+⋯+yC(n)logy^C(n)]=−∑c=1Cyc(n)log(y^c(n))
考虑全部训练样本,基于交叉熵损失函数,模型在训练集上的风险函数为:
R(W)=−N1n=1∑Nc=1∑Cyc(n)logy^c(n)=−N1n=1∑N(y(n))⊤logy^(n)
- 优化算法:使用梯度下降,针对的是 w,上述与该项有关系的只有 y^(n)。
∂W∂R(W)=−N1n=1∑Nx(n)(y(n)−y^(n))⊤
Wt+1←Wt+α(N1n=1∑Nx(n)(y(n)−y^Wt(n))⊤)
| 要素 |
公式 |
| 模型 |
p(y=c∣x)=softmax(wcTx)=∑i=1Cexp(wi⊤x)exp(wc⊤x) |
| 学习准则 |
R(W)=−N1∑n=1N(y(n))⊤logy^(n) |
| 优化算法 |
∂W∂R(W)=−N1∑n=1Nx(n)(y(n)−y^(n))⊤Wt+1←Wt+α(N1∑n=1Nx(n)(y(n)−y^Wt(n))⊤) |
感知机
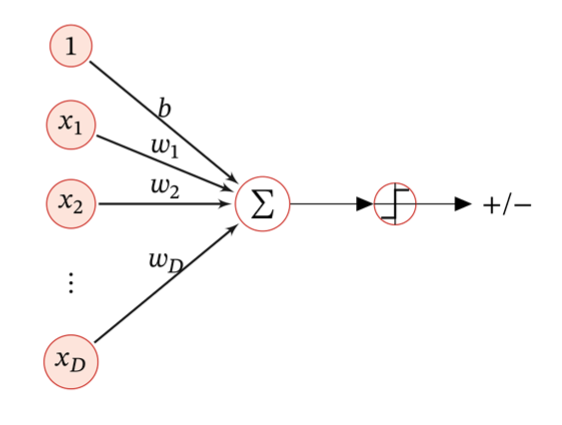
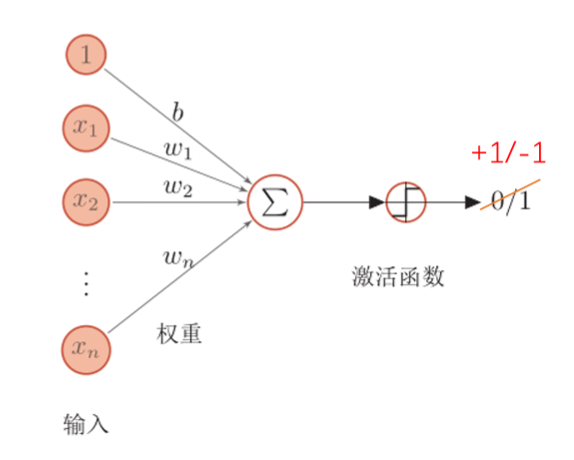
感知机(Perceptron)由 FrankRoseblatt 于1957年提出,是一种广泛使用的线性分类器。感知器可谓是最简单的人工神经网络,只有一个神经元。模拟生物神经元行为的机器,有与生物神经元相对应的部件:
| 生物神经元部件 |
感知机组成 |
| 突触 |
权重 |
| 阈值 |
偏置 |
| 细胞体 |
激活函数 |
g(x,w)={+1−1 当 wTx>0, 当 wTx<0.
L(w;x,y)=max(0,−ywTx)
∂w∂L(w;x,y)={0−yx 当 ywTx>0, 当 ywTx<0.
当 ywTx<0wk+1←wk+yx
线性分类模型小结
| 线性模型 |
激活函数 |
损失函数 |
优化方法 |
| 线性回归 |
- |
(y−w⊤x)2 |
梯度下降 |
| Logistic 回归 |
σ(w⊤x) |
ylogσ(w⊤x) |
梯度下降 |
| Softmax 回归 |
softmax(W⊤x) |
ylogsoftmax(W⊤x) |
梯度下降 |
| 感知机 |
sgn(w⊤x) |
max(0,−yw⊤x) |
随机梯度下降 |