递归与分治

递归程序

  • 用函数自身给出的定义的函数：递归函数

    一个递归函数的两个基本要素：

    • 递归边界
    • 递归关系式

  • 直接或间接调用自身的程序：递归程序

    一个递归程序的两个部分：

    • 边界处理部分
    • 递归调用部分

阶乘 N

问题分析

递归函数：

  1. 当 N⩾1N \geqslant 1 时，N!=N×(N−1)!N !=N \times(N-1) !
  2. 当 N=0N =0 时，N!=0!=1N !=0!=1

将两个要素合并就是：

N!={1N=0N(N−1)!N>0N != \begin{cases}1 & N=0 \\ N(N-1) ! & N>0\end{cases}

算法设计与实现

递归程序：

1
2
3
4
int factorial(int n){
	if(n== 0) return 1;//递归边界
	return n* factorial(n-1);
}

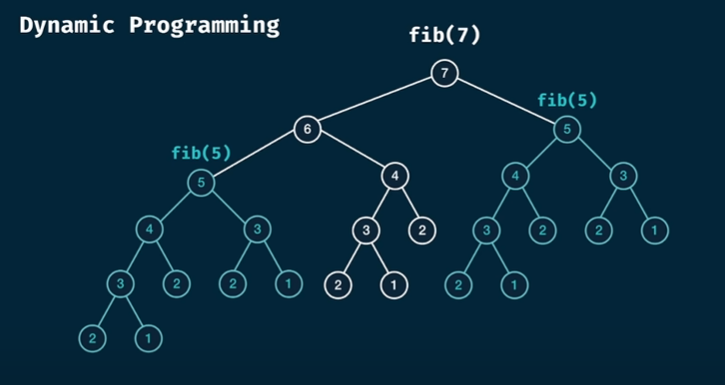
Fibonacci 数列

问题分析

第 11 个月，兔子 11 对；

第 22 个月，兔子 11 对；

第 33 个月，兔子 22 对；

第 44 个月，兔子 33 对；

第 55 个月，兔子 55 对；

⋯\cdots

第 nn 个月，第 n−1n-1 个月的兔子对数 + 第 n−2n-2 个月的兔子个数

递归函数：

F(n)={1n=1,2F(n−1)+F(n−2)n>2F(n)= \begin{cases}1 & n=1,2 \\ F(n-1)+F(n-2) & n>2\end{cases}

算法设计与实现

算法设计与实现

1
2
3
4
5
6
long Fib(int n)
{
    if (n <= 2)
        return 1;
    return Fib(n - 1) + Fib(n - 2);
}

Stirling 数

问题分析

S(n,m)S(n,m)：将 nn 个元素划分成 mm 个非空子集种类。

  • 将n−1n-1个元素的集合划分成mm个非空子集，再将剩下的一个元素插入到mm个子集中的任意一个：m×S(n−1,m)m \times S(n-1, m)；
  • 将n−1n-1个元素的集合划分成m−1m-1个非空子集，再将剩下的一个元素作为一个独立子集：S(n−1,m−1)S(n-1, m-1)；

当 m=0m=0 或 m>nm>n，有 00 种划分。

当 m=1m=1 或 m=nm=n，有 11 种划分。

递归函数：

S(n,m)={0m=0 or m>n1m=1 or m=nm×S(n−1,m)+S(n−1,m−1)0<m<nS(n, m)= \begin{cases}0 & m=0 \text { or } m>n \\ 1 & m=1 \text { or } m=n \\ m \times S(n-1, m)+S(n-1, m-1) & 0<m<n\end{cases}

算法设计与实现

1
2
3
4
5
6
7
8
long Stirling(int n, int m)
{
    if ((m == n) || (m == 1))
        return 1;
    if ((m > n) || (m == 0))
        return 0;
    return m * Stirling(n - 1, m) + Stirling(n - 1, m - 1);
}

整数划分

问题分析

C(n,m)C(n,m)：最大加数 n1n_1 不大于 mm 的划分个数。

  • 最大加数 n1=mn_1=m 的划分：C(n−m,m)C(n-m, m)；
  • 最大加数 n1≤m−1n_1 \leq m-1 的划分：C(n,m−1)C(n, m-1)；

C(n,1)=1C(n,1)=1；

C(1,m)=1C(1,m)=1；

当 m>nm>n 时，C(n,m)=C(n,n)C(n,m)=C(n,n)。

递归函数：

C(n,m)={1,m=1 or n=1C(n,n)m>nC(n−m,m)+C(n,m−1)1<m⩽nC(n, m)= \begin{cases}1, & m=1 \text { or } n=1 \\ C(n, n) & m>n \\ C(n-m, m)+C(n, m-1) & 1<m \leqslant n\end{cases}

算法设计与实现

1
2
3
4
5
6
7
8
long C(int n, int m)
{
    if ((n == 1) == (m == 1))
        return 1;
    if (n < m)
        return C(n, n);
    return C(n, m - 1) + C(n - m, m);
}

分治策略

分治：将一个规模为 nn 的大问题分解为 kk 个规模较小的子问题，子问题相互独立并且与原问题性质相同，然后递归地求解子问题，最后将各个子问题的解合并得到原问题的解。

黑盒划分典型问题

合并排序

问题分析

分：A={a[l],⋯ ,a[r]}A=\{a[l], \cdots, a[r]\}

  • A1={a[l],⋯ ,a[⌊(l+r)/2⌋}A_1=\{a[l], \cdots, a[\lfloor(l+r) / 2\rfloor\}
  • A2={a[⌊(l+r)/2⌋+1],⋯ ,a[r]}A_2=\{a[\lfloor(l+r) / 2\rfloor+1], \cdots, a[r]\}

治：若 ∣Ai∣=1|A_i|=1，将 AiA_i 视作已经排好序的集合；否则继续分割集合。

合：合并按升序排列的子集 B1B_1 和 B2B_2 成一个整体升序排列的集合 BB。

算法实现与分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <cstdio>

int iDatas[10000];
int iBuffer[10000];

void merge(int, int, int);
void mergeSort(int, int);

void merge(int iLow, int iMid, int iHigh)
{
    int i = iLow, j = iMid + 1, k = iLow;
    while ((i <= iMid) && (j <= iHigh))
    {
        if (iDatas[i] <= iDatas[j])
            iBuffer[k++] = iDatas[i++];
        else
            iBuffer[k++] = iDatas[j++];
    }
    if (i <= iMid)
        for (int ii = i; ii <= iMid; ii++)
            iBuffer[k++] = iDatas[ii];
    else
        for (int jj = j; jj <= iHigh; jj++)
            iBuffer[k++] = iDatas[jj];
}

void mergeSort(int iLow, int iHigh)
{
    if (iHigh > iLow)
    {
        int iMid = (iLow + iHigh) / 2;
        mergeSort(iLow, iMid);
        mergeSort(iMid + 1, iHigh);
        merge(iLow, iMid, iHigh);
        for (int i = iLow; i <= iHigh; i++)
            iDatas[i] = iBuffer[i];
    }
}

int main()
{
    int iNum = 0;
    scanf("%d", &iNum);
    while (iNum != -1)
    {
        for (int i = 0; i < iNum; i++)
            scanf("%d", &iDatas[i]);
        mergeSort(0, iNum - 1);
        for (int i = 0; i < iNum; i++)
            printf("%d ", iDatas[i]);
        printf("\r\n");
        scanf("%d", &iNum);
    }
    return 0;
}

mergeSort递归过程是将待排序集合一分为二，直至待排序集合只剩下一个元素位为止，然后不断合并两个排好序的相邻子集合，可以采用两两配对来消除递归后：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <iostream>
#include <cstdio>

int iDatas[10000];
int iBuffer[10000];

void merge(int, int, int);
void mergeSort(int, int);
void mergeSort2(int);

void merge(int iLow, int iMid, int iHigh)
{
    int i = iLow, j = iMid + 1, k = iLow;
    while ((i <= iMid) && (j <= iHigh))
    {
        if (iDatas[i] <= iDatas[j])
            iBuffer[k++] = iDatas[i++];
        else
            iBuffer[k++] = iDatas[j++];
    }
    if (i <= iMid)
        for (int ii = i; ii <= iMid; ii++)
            iBuffer[k++] = iDatas[ii];
    else
        for (int jj = j; jj <= iHigh; jj++)
            iBuffer[k++] = iDatas[jj];
}

void mergeSort(int iLow, int iHigh)
{
    if (iHigh > iLow)
    {
        int iMid = (iLow + iHigh) / 2;
        mergeSort(iLow, iMid);
        mergeSort(iMid + 1, iHigh);
        merge(iLow, iMid, iHigh);
        for (int i = iLow; i <= iHigh; i++)
            iDatas[i] = iBuffer[i];
    }
}

void mergeSort2(int iLen)
{
    int iStep = 1;
    while (iStep < iLen)
    {
        int i = 0;
        while (i <= (iLen - 2 * iStep))
        {
            merge(i, i + iStep - 1, i + 2 * iStep - 1);
            i = i + 2 * iStep;
        }
        if (i + iStep < iLen)
            merge(i, i + iStep - 1, iLen - 1);
        else
            for (int j = i; j < iLen; j++)
                iBuffer[j] = iDatas[j];
        for (int j = 0; j < iLen; j++)
            iDatas[j] = iBuffer[j];
        iStep += iStep;
    }
}

int main()
{
    int iNum = 0;
    scanf("%d", &iNum);
    while (iNum != -1)
    {
        for (int i = 0; i < iNum; i++)
            scanf("%d", &iDatas[i]);
        mergeSort2(iNum);
        for (int i = 0; i < iNum; i++)
            printf("%d ", iDatas[i]);
        printf("\r\n");
        scanf("%d", &iNum);
    }
    return 0;
}

逆序对

问题分析

分：A={a[l],⋯ ,a[r]}A=\{a[l], \cdots, a[r]\}

  • A1={a[l],⋯ ,a[⌊(l+r)/2⌋}A_1=\{a[l], \cdots, a[\lfloor(l+r) / 2\rfloor\}
  • A2={a[⌊(l+r)/2⌋+1],⋯ ,a[r]}A_2=\{a[\lfloor(l+r) / 2\rfloor+1], \cdots, a[r]\}

治：若 ∣Ai∣=1|A_i|=1，AiA_i 没有逆序对，返回 00；否则继续分割集合。

合：

原数组 AA 的逆序对分为三个部分：

  1. 子数组 A1A_1 中的逆序对，数目 C1C_1
  2. 子数组 A2A_2 中的逆序对，数目 C2C_2
  3. A[i]∈A1A[i] \in A_1，A[j]∈A2A[j] \in A_2，(A[i],A[j])(A[i], A[j]) 数目 C3C_3

可以选择将子数组 A1A_1 和A2A_2 按照升序排序，

  • A1[i]>A2[j]⇒A1[i+1]>A2[j],⋯ ,A1[ L(l+r)/2⌋]>A2[j]⇒⌊(l+r)/2⌋−i+1A_1[i]>A_2[j] \Rightarrow \left.A_1[i+1]>A_2[j], \cdots, A_1[\mathrm{~L}(l+r) / 2\rfloor\right]>A_2[j] \Rightarrow \lfloor(l+r) / 2\rfloor-i+1 个逆序对；
  • A1[i]≤A2[j]A_1[i] \leq A_2[j]，A1[i]A_1[i] 及其之后元素不与 A2[j]A_2[j] 构成逆序对。

算法实现与分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <cstdio>

int iDatas[10000];
int iBuffer[10000];

long mergeReverse(int, int, int);
long reverseOrderPairs(int, int);

long mergeReverse(int iLow, int iMid, int iHigh)
{
    int i = iLow, j = iMid + 1, k = iLow;
    long iCrossPairs = 0;
    while ((i <= iMid) && (j <= iHigh))
    {
        if (iDatas[i] <= iDatas[j])
            iBuffer[k++] = iDatas[i++];
        else
        {
            iCrossPairs += iMid - i + 1;
            iBuffer[k++] = iDatas[j++];
        }
    }
    if (i <= iMid)
        for (int ii = i; ii <= iMid; ii++)
            iBuffer[k++] = iDatas[ii];
    else
        for (int jj = j; jj <= iHigh; jj++)
            iBuffer[k++] = iDatas[jj];
    return iCrossPairs;
}

long reverseOrderPairs(int iLow, int iHigh)
{
    if (iLow == iHigh)
        return 0;
    int iMid = (iLow + iHigh) / 2;
    long C1, C2, C3;
    C1 = reverseOrderPairs(iLow, iMid);
    C2 = reverseOrderPairs(iMid + 1, iHigh);
    C3 = mergeReverse(iLow, iMid, iHigh);
    for (int i = iLow; i <= iHigh; i++)
        iDatas[i] = iBuffer[i];
    long C = C1 + C2 + C3;
    return C;
}

int main()
{
    int iNum = 0;
    long iReversePairsNum = 0;
    scanf("%d", &iNum);
    while (iNum != -1)
    {
        for (int i = 0; i < iNum; i++)
            scanf("%d", &iDatas[i]);
        iReversePairsNum = reverseOrderPairs(0, iNum - 1);
        printf("%d ", iReversePairsNum);
        printf("\r\n");
        scanf("%d", &iNum);
    }
    return 0;
}

白盒划分典型问题

快速排序

问题分析

分：A={a[l],⋯ ,a[r]}A=\{a[l], \cdots, a[r]\}：以 a[l]a[l] 为基准元素

  • A1={a′[l],⋯ ,a′[k−1]}A_1=\left\{a^{\prime}[l], \cdots, a^{\prime}[k-1]\right\}：所有元素小于等于基准元素 a[l]a[l]
  • A2={a′[k]}A_2=\left\{a^{\prime}[k]\right\}：调整位置后的基准元素 a[l]a[l]
  • A3={a′[k+1],⋯ ,a′[r]}A_3=\left\{a^{\prime}[k+1], \cdots, a^{\prime}[r]\right\}：所有元素大于等于基准元素 a[l]a[l]

治：若 ∣Ai∣=1(i=1,3)|A_i|=1(i=1,3)，AiA_i 已排好序的集合；否则继续分割集合。A2A_2 保持不变。

合：序列 [A1,A2,A3][A_1,A_2,A_3] 有序。

算法实现与分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <iostream>
#include <cstdio>

int iDatas[10000];
int iBuffer[10000];

int partition(int, int);
void quickSort(int, int);
void swap(int &, int &);

int partition(int iLeft, int iRight)
{
    int i = iLeft + 1, j = iRight;
    int iAnchor = iDatas[iLeft];
    while (i <= j)
    {
        while ((iDatas[i] <= iAnchor) && (i <= iRight))
            i++;
        while ((iDatas[j] > iAnchor) && (j >= iLeft))
            j--;
        if (i < j)
        {
            swap(iDatas[i], iDatas[j]);
            i++;
            j--;
        }
    }
    swap(iDatas[iLeft], iDatas[j]);
    return j;
}

void quickSort(int iLeft, int iRight)
{
    if (iRight > iLeft)
    {
        int k = partition(iLeft, iRight);
        quickSort(iLeft, k - 1);
        quickSort(k + 1, iRight);
    }
}

void swap(int &iValue1, int &iValue2)
{
    int iTemp = iValue1;
    iValue1 = iValue2;
    iValue2 = iTemp;
}

int main()
{
    int iNum = 0;
    scanf("%d", &iNum);
    while (iNum != -1)
    {
        for (int i = 0; i < iNum; i++)
            scanf("%d", &iDatas[i]);
        quickSort(0, iNum - 1);
        for (int i = 0; i < iNum; i++)
            printf("%d ", iDatas[i]);
        printf("\r\n");
        scanf("%d", &iNum);
    }
    return 0;
}

快速排序算法的性能取决于划分的对称性，可以采用随机选择基准元素的策略改善算法效率。

在概率意义上，期待更多的划分是对称的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>
#include <cstdio>

int iDatas[10000];
int iBuffer[10000];

int partition(int, int);
void randomizedQuickSort(int, int);
void swap(int &, int &);

int partition(int iLeft, int iRight)
{
    int i = iLeft + 1, j = iRight;
    int iAnchor = iDatas[iLeft];
    while (i <= j)
    {
        while ((iDatas[i] <= iAnchor) && (i <= iRight))
            i++;
        while ((iDatas[j] > iAnchor) && (j >= iLeft))
            j--;
        if (i < j)
        {
            swap(iDatas[i], iDatas[j]);
            i++;
            j--;
        }
    }
    swap(iDatas[iLeft], iDatas[j]);
    return j;
}

void randomizedQuickSort(int iLeft, int iRight)
{
    if (iRight > iLeft)
    {
        srand((unsigned)time(NULL));
        int iAncharIndex = rand() % (iRight - iLeft + 1) + iLeft;
        swap(iDatas[iAncharIndex], iDatas[iLeft]);
        int k = partition(iLeft, iRight);
        randomizedQuickSort(iLeft, k - 1);
        randomizedQuickSort(k + 1, iRight);
    }
}

void swap(int &iValue1, int &iValue2)
{
    int iTemp = iValue1;
    iValue1 = iValue2;
    iValue2 = iTemp;
}

int main()
{
    int iNum = 0;
    scanf("%d", &iNum);
    while (iNum != -1)
    {
        for (int i = 0; i < iNum; i++)
            scanf("%d", &iDatas[i]);
        randomizedQuickSort(0, iNum - 1);
        for (int i = 0; i < iNum; i++)
            printf("%d ", iDatas[i]);
        printf("\r\n");
        scanf("%d", &iNum);
    }
    return 0;
}

最接近点

问题分析

🅰一维情况：x1,⋯ ,xnx_{1}, \cdots, x_{n}

基于平衡子问题原则，用 SS 中各点坐标的中位数 mm 做分割点，分割后的子集 S1S_1 和 S2S_2 大致相同。

递归地在S1S_1和S2S_2中找到最接近的点对 (p1,p2)\left(p_{1}, p_{2}\right)，(q1,q2)\left(q_{1}, q_{2}\right)，且令

d=min⁡(∣p1−p2∣,∣q1−q2∣)d=\min \left(\left|p_{1}-p_{2}\right|,\left|q_{1}-q_{2}\right|\right)

如果 SS 的最接近点对是 (p3,q3)(p_3,q_3)，有 ∣p3−q3∣<d\left|p_{3}-q_{3}\right|<d

则 p3∈S1p_{3} \in S_{1}，q3∈S2q_{3} \in S_{2}，即 p3∈(m−d,m]p_{3} \in(m-d, m]，q3∈(m,m+d]q_{3} \in(m, m+d]。

在 S1S_1（S2S_2） 中，每个长度为 dd 的区间至多包含一个点（否则必有两点举例小于（大于） dd），因此

  • 如果 (m−d,m](m-d, m] 中有 SS 中的点，此点就是 S1S_1 的最大点
  • 如果 (m,m+d](m, m+d] 中有 SS 中的点，此点就是 S2S_2 的最小点

🅱二维情况：

基于平衡子问题原则，用 SS 中各点 XX 轴坐标的中位数 mm 选取一垂直线 L:x=mL: x=m 作为平面上点集 SS 的分割线，分割后的子集 S1S_1 和 S2S_2 大致相同。

  • S1={p∈S∣x(p)⩽m}S_{1}=\{p \in S \mid x(p) \leqslant m\}
  • S2={p∈S∣x(p)>m}S_{2}=\{p \in S \mid x(p)>m\}

递归地在子集 S1S_1 和 S2S_2 上求解最接近点对问题，分别求得 S1S_1 和 S2S_2 中的最小距离分别为 d1d_1 和 d2d_2，且令

d=min⁡(d1,d2)d=\min \left(d_1, d_2\right)

如果 SS 的最接近点对是 (p,q)(p,q)，，有 ∣p−q∣<d\left|p-q\right|<d

则 p∈S1p \in S_{1}，q∈S2q \in S_{2}。

进一步假设 P1P_1 和 P2P_2 分别表示直线 LL 的左边和右边宽度为 dd 的两个垂直区域。

1⃣从几何角度分析，给定 P1P_1 中的点 pp，P2P_2中满足 Dis⁡(p,q)<d\operatorname{Dis}(p, q)<d 的点 qq 一定在 d×2dd \times 2 d 的矩形 RR 中。

2⃣P2P_2 中任何两个 S2S_2 中点的距离都不小于 d⇒d \Rightarrow 矩形 RR 中最多只有 66 个 S2S_2 中的点。

算法实现与分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
#include <iostream>
#include <cstdio>
#include <cmath>
#define N 100000
#define eps 1e-15

struct Point
{
    double x, y;
    int index;
};

Point psSortX[N], psSortY[N], psBuff[N];

double closestPair(Point *, Point *, Point *, int, int);
double calDistance(Point, Point);
int cmpX(const void *, const void *);
int cmpY(const void *, const void *);
int merge(Point *, Point *, int, int, int);
inline double min(double, double);

// double closestPair(Point psSrc[], Point psSortY[], Point psBuff[], int ptrFirst, int ptrLast)
double closestPair(Point *psSrc, Point *psSortY, Point *psBuff, int ptrFirst, int ptrLast)
{
    if (ptrLast - ptrFirst == 1)
        return calDistance(psSrc[ptrFirst], psSrc[ptrLast]);
    if (ptrLast - ptrFirst == 2)
    {
        double dis1 = calDistance(psSrc[ptrFirst], psSrc[ptrLast]);
        double dis2 = calDistance(psSrc[ptrFirst + 1], psSrc[ptrLast]);
        double dis3 = calDistance(psSrc[ptrFirst], psSrc[ptrFirst + 1]);
        if (dis1 < dis2 && dis1 < dis3)
            return dis1;
        else if (dis2 < dis3)
            return dis2;
        else
            return dis3;
    }
    int m = (ptrFirst + ptrLast) / 2;
    for (int i = ptrFirst, j = ptrFirst, k = m + 1; i <= ptrLast; i++)
    {
        if (psSortY[i].index <= m)
            psBuff[j++] = psSortY[i];
        else
            psBuff[k++] = psSortY[i];
    }
    double d1, d2;
    d1 = closestPair(psSrc, psBuff, psSortY, ptrFirst, m);
    d2 = closestPair(psSrc, psBuff, psSortY, m + 1, ptrLast);
    double dm = min(d1, d2);
    merge(psSortY, psBuff, ptrFirst, m, ptrLast);
    int k;
    for (int i = ptrFirst, k = ptrFirst; i <= ptrLast; i++)
        if (fabs(psSortY[i].x - psSortY[m].x) < dm)
            psBuff[k++] = psSortY[i];
    for (int i = ptrFirst; i < k; i++)
        for (int j = i + 1; j < k && psBuff[j].y - psBuff[i].y < dm; j++)
        {
            double temp = calDistance(psBuff[i], psBuff[j]);
            if (temp < dm)
                dm = temp;
        }
    return dm;
}

double calDistance(Point p, Point q)
{
    double x = p.x - q.x;
    double y = p.y - q.y;
    return sqrt(x * x + y * y);
}

int cmpX(const void *p, const void *q)
{
    double temp = ((Point *)p)->x - ((Point *)q)->x;
    if (temp > eps)
        return 1;
    else if (fabs(temp) < eps)
        return 0;
    else
        return -1;
}

int cmpY(const void *p, const void *q)
{
    double temp = ((Point *)p)->y - ((Point *)q)->y;
    if (temp > eps)
        return 1;
    else if (fabs(temp) < eps)
        return 0;
    else
        return -1;
}

// int merge(Point psDst[], Point psSrc[], int first, int mid, int last)
int merge(Point *psDst, Point *psSrc, int first, int mid, int last)
{
    int i, j, k;
    for (i = first, j = mid + 1, k = first; i <= mid && j <= last;)
    {
        if (psSrc[i].y > psSrc[j].y)
            psDst[k++] = psSrc[j++];
        else
            psDst[k++] = psSrc[i++];
    }
    while (i <= mid)
        psDst[k++] = psSrc[i++];
    while (j <= last)
        psDst[k++] = psSrc[i++];
    memcpy(psSrc + first, psDst + first, (last - first + 1) * sizeof(psDst[0]));
    return 0;
}

inline double min(double p, double q)
{
    return (p > q) ? (q) : (p);
}

int main()
{
    int n;
    double d;
    scanf("%d", &n);
    while (n != -1)
    {
        for (int i = 0; i < n; i++)
            scanf("%lf %lf", &(psSortX[i].x), &(psSortX[i].y));
        qsort(psSortX, n, sizeof(psSortX[0]), cmpX);
        for (int i = 0; i < n; i++)
            psSortX[i].index = i;
        memcpy(psSortY, psSortX, n * sizeof(psSortX[0]));
        qsort(psSortY, n, sizeof(psSortY[0]), cmpY);
        d = closestPair(psSortX, psSortY, psBuff, 0, n - 1);
        printf("%.2lf\n", d);
        scanf("%d", &n);
    }
    return 0;
}

减治策略

指数运算

问题分析

递归方程

an={(an/2)2n 是偶数 a×(a(n−1)/2)2n 是奇数 an=1a^n= \begin{cases}\left(a^{n / 2}\right)^2 & n \text { 是偶数 } \\ a \times\left(a^{(n-1) / 2}\right)^2 & n \text { 是奇数 } \\ a & n=1\end{cases}

算法实现与分析

复杂性为 O(log⁡n)O(\log n) 的指数运算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <cmath>
#include <cstdio>
#define eps 1e-15

double powerF1(double, int);

double powerF1(double a, int n)
{
    if (n == 1)
        return a;
    double rst;
    if (n % 2 == 0)
    {
        rst = powerF1(a, n / 2);
        return rst * rst;
    }
    else
    {
        rst = powerF1(a, (n - 1) / 2);
        return rst * rst * a;
    }
}

int main()
{
    double a;
    int n;
    scanf("%lf", &a);
    while (fabs(a - (-1.0)) > eps)
    {
        scanf("%d", &n);
        double result = powerF1(a, n);
        printf("%.2lf ", result);
        printf("\r\n");
        scanf("%lf", &a);
    }
    return 0;
}

复杂性为 O(n)O(n) 的指数运算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <cmath>
#include <cstdio>
#define eps 1e-15

double powerF1(double, int);

double powerF1(double a, int n)
{
    if (n == 1)
        return a;
    if (n % 2 == 0)
        return powerF1(a, n / 2) * powerF1(a, n / 2);
    else
        return powerF1(a, n / 2) * powerF1(a, n / 2) * a;
}

int main()
{
    double a;
    int n;
    scanf("%lf", &a);
    while (fabs(a - (-1.0)) > eps)
    {
        scanf("%d", &n);
        double result = powerF1(a, n);
        printf("%.2lf ", result);
        printf("\r\n");
        scanf("%lf", &a);
    }
    return 0;
}

二分查找

分为非递归实现和递归实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <cstdio>

int iDatas[10000];

int BinarySearch(int[], int, int);
int BinarySearch_Recursive(int[], int, int, int);

int BinarySearch(int array[], int len, int value)
{
    if (array == NULL || len <= 0)
        return -1;
    int low = 0;
    int high = len - 1;
    while (low <= high)
    {
        int mid = low + (high - low) / 2;
        if (array[mid] == value)
            return mid;
        else if (array[mid] > value)
            high = mid - 1;
        else
            low = mid + 1;
    }
    return -1;
}

int BinarySearch_Recursive(int array[], int low, int high, int value)
{
    if (low > high)
        return -1;
    int mid = low + (high - low) / 2;
    if (array[mid] == value)
        return mid;
    else if (array[mid] > value)
        return BinarySearch_Recursive(array, low, mid - 1, value);
    else
        return BinarySearch_Recursive(array, mid + 1, high, value);
}

int main()
{
    int iNum, search;
    scanf("%d", &search);
    while (search != -1)
    {
        scanf("%d", &iNum);
        for (int i = 0; i < iNum; i++)
            scanf("%d", &iDatas[i]);
        int location = BinarySearch(iDatas, iNum, search);
        printf("%d ", location);
        printf("\r\n");
        scanf("%d", &search);
    }
    return 0;
}