动态规划

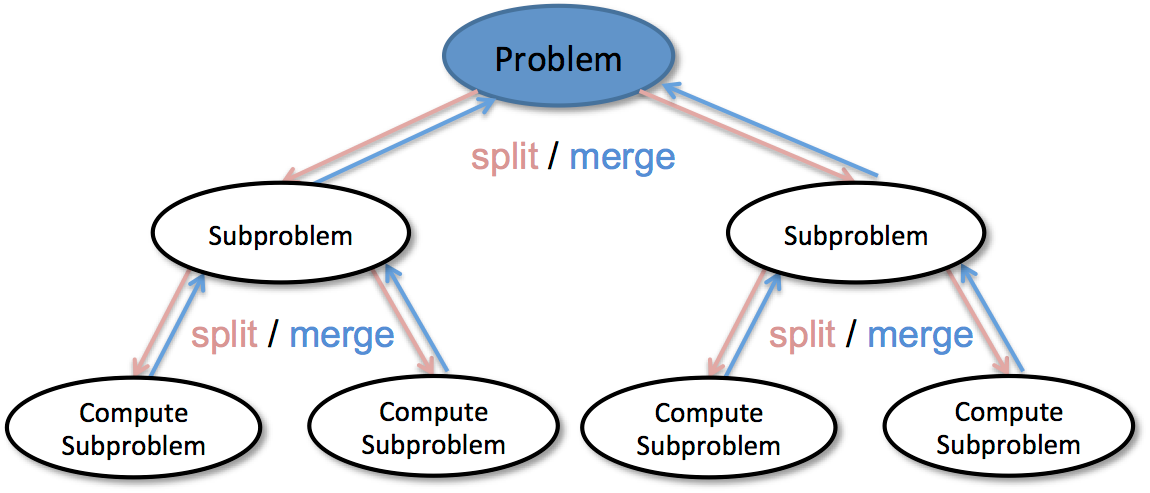
动态规划的关键在于解决重叠子问题的重复计算，以空间换时间的策略解决指数级复杂度的分治算法，改为多项式级的时间复杂度。

动态规划算法并非适用与所有的最优化问题，适用与动态规划求解的问题应该具备两个基本要素：最优子结构性质和子问题重叠性质。

最优子结构性质：问题的最优解包含其他子问题的最优解，问题的最优解分解（两个部分或多个部分、删除第一个或最后一个分量），得到的子问题的解 $\rightarrow$ 该子问题的解也是特定子问题的最优解。

子问题重叠性质：每次产生的子问题并不总是新问题，有些子问题重复出现。第 $1$ 次执行，执行求解过程，记录求解结果。第 $n$ 次执行，从记录中引用答案。

求解步骤

1. 分析最优子结构性质：分析和描述该子解对应的子问题，证明该子解是对应子问题的最优解，该问题满足最优子结构性质；
   • 基于划分的方法：问题的最优解依据问题性质划分为两个或多个子解
   • 基于减一的方法：问题的最优解依据问题性质缩减规模
     • 减去最优解的第一个分量
     • 减去最优解的最后一个分量
2. 确定状态表示和状态递推方程，递归定义最优值；
3. 确定状态转移顺序，以自底向上的方式计算出最优值；
4. 根据计算最优值时得到的信息，构造最优解。

三类典型问题的动态规划算法：

1. 基于划分策略构造子问题最优值与原问题最优值的递推关系
   • 矩阵连乘
   • 最优二叉搜索树
2. 基于减一策略构造子问题最优值与原问题最优值得递推关系
   • 多段图最短路径
   • 最长公共子序列
   • 0-1背包问题
3. 状态值不是直接表示待求节问题的目标值，定义中间目标，通过中间目标值计算出原问题的最优值
   • 最大上升子序列

矩阵连乘

问题描述：给定 $n$个数字矩阵 $\boldsymbol{A}_{1}$, $\boldsymbol{A}_{2}$, $\cdots$, $\boldsymbol{A}_{n}$，其中 $\boldsymbol{A}_{i}$ 与 $\boldsymbol{A}_{i+1}$ 是可乘的，$i=1,2, \cdots, n-1$。用加括号的方式表示矩阵连乘的次序，不同的加括号方法所对应的计算次序是不同的，所需要的数乘次数也是不一样的。

1⃣两个矩阵相乘 $\boldsymbol{C}=\boldsymbol{A B}$

$\boldsymbol{A}$：$p \times r$，$\boldsymbol{B}$：$r \times q$ ⇒ $\boldsymbol{C}$：$p \times q$

其中 $(i,j)$ 元素为：$c_{i j}=\sum_{k=1}^{r} a_{i k} b_{k j}$，$i=1, \cdots, p, j=1, \cdots, q$

$\boldsymbol{A B}$ 所用数乘的次数为 $p \times r \times q$

2⃣三个矩阵相乘 $\left(\left(\boldsymbol{A}_1 \boldsymbol{A}_2\right) \boldsymbol{A}_3\right)$ 和 $\left(\boldsymbol{A}_1\left(\boldsymbol{A}_2 \boldsymbol{A}_3\right)\right)$

• $\boldsymbol{A}_1$：$p_{0} \times p_{1}$
• $\boldsymbol{A}_2$：$p_{1} \times p_{2}$
• $\boldsymbol{A}_3$：$p_{2} \times p_{3}$

次数

• $\left(\left(\boldsymbol{A}_1 \boldsymbol{A}_2\right) \boldsymbol{A}_3\right)$ 所用数乘次数 $p_{0} p_{1} p_{2}+p_{0} p_{2} p_{3}$
• $\left(\boldsymbol{A}_1\left(\boldsymbol{A}_2 \boldsymbol{A}_3\right)\right)$ 所用数乘次数 $p_{0} p_{1} p_{3}+p_{1} p_{2} p_{3}$

任意给定 $n$ 个可乘的数字矩阵 $\boldsymbol{A}_{1}, \boldsymbol{A}_{2}, \cdots, \boldsymbol{A}_{n}$，以及矩阵的阶 $p_{0} \times p_{1}, p_{1} \times p_{2}, \cdots, p_{n-1} \times p_{n}$，求解给定矩阵练的最优计算次序使得所需要的数乘次数最少。

输入：多组测试数据，每组数据包含两行

• 第一行矩阵个数 $n(n<1000)$
• 第二行输入 $n+1$ 个数，依次表示 $p_{0}, p_{1}, \cdots, p_{n}$

输出：最少的数乘次数。

问题分析

🔴最优子结构：假设 $n$个矩阵连乘的最优加括号方案为 $\left(\left(\boldsymbol{A}_{1} \cdots \boldsymbol{A}_{k}\right)\left(\boldsymbol{A}_{k+1} \cdots \boldsymbol{A}_{n}\right))\right)$（省略了内部子矩阵链加括号方案），则加括号方案 $\left(\boldsymbol{A}_{1} \cdots \boldsymbol{A}_{k}\right)$ 是子矩阵链 $\boldsymbol{A}_{1} \cdots \boldsymbol{A}_{k}$ 最优加括号方案，$\left(\boldsymbol{A}_{k+1} \cdots \boldsymbol{A}_{n}\right)$ 是 $\boldsymbol{A}_{k+1} \cdots \boldsymbol{A}_{n}$ 的最优加括号方案。

⚫状态表示和状态递推方程：每一个子矩阵链 $\boldsymbol{A}_{i} \cdots \boldsymbol{A}_{j}$ 对应一个子问题 $\boldsymbol{A}[i: j]$，它的最优计算次序对应的乘法次数表示为 $m(i, j)$，$1 \leqslant i, j \leqslant n$（原问题的最优值为 $m(1,n)$）。

1. 当 $i=j$，单一矩阵，无需计算，$m(i, i)=0,1 \leqslant i \leqslant n$
2. 当 $i<j$，利用最优子结构性来计算，$m(i, j)=m(i, k)+m(k+1, j)+p_{i-1} p_{k} p_{j}$

对于情况 $2$，划分的位置不同，对应求得的最优值可能不同，故

$m(i, j)= \begin{cases}0 & i=j \\ \min _{i \leqslant k<j}\left\{m(i, k)+m(k+1, j)+p_{i-1} p_k p_j\right\} & i<j\end{cases}$

🔵计算最优值：依据状态转移方程以自底向上的方式进行计算。

• 保存已解决的子问题答案；
• 后续待解决的问题从保存的空间中读取。

$s(i,j)=k$：矩阵链 $\boldsymbol{A}[i: j]$ 最佳方式是在 $\boldsymbol{A}_{k}$ 和 $\boldsymbol{A}_{k+1}$ 之间断开，形如 $(\boldsymbol{A}[i: k])(\boldsymbol{A}[k+1: j])$。自顶向下地构造矩阵链的最优完全加括号方案

$\boldsymbol{A}[1: n]$的最优加括号方式：$s(1,n)$ ⇒ $\left(\left(\boldsymbol{A}_{1} \cdots \boldsymbol{A}_{s(1, n)}\right)\left(\boldsymbol{A}_{s(1, n)+1} \cdots \boldsymbol{A}_{n}\right)\right)$

• $\boldsymbol{A}[1: s(1,n)]$的最优加括号方式：$q=s(1,s(1,n))$ ⇒ $\left(\left(\boldsymbol{A}_{1} \cdots \boldsymbol{A}_{q}\right)\left(\boldsymbol{A}_{q+1} \cdots \boldsymbol{A}_{s(1, n)}\right)\right)$
• $\boldsymbol{A}[s(1,n):n ]$的最佳开括号方式：$r=s(s(1,n),n)$ ⇒ $\left(\left(\boldsymbol{A}_{s(1,n)+1} \cdots \boldsymbol{A}_{r}\right)\left(\boldsymbol{A}_{r+1} \cdots \boldsymbol{A}_{n}\right)\right)$

依次类推下去，最终可以确定 $\boldsymbol{A}[1: n]$ 的完整最优加括号方式。

算法实现与分析

矩阵连乘的动态规划算法：

#include <stdio.h>
#include <string.h>
#define MaxNum 1000

long MatrixChain(int);
int dim[MaxNum];
long memoTable[MaxNum][MaxNum];
int bestK[MaxNum][MaxNum];

long MatrixChain(int);

long MatrixChain(int matrixNum)
{
    int i, j, len, k;
    for (i = 1; i <= matrixNum; i++)
        memoTable[i][i] = 0;
    for (len = 2; len <= matrixNum; len++)
    {
        for (i = 1; i <= matrixNum - len + 1; i++)
        {
            j = i + len - 1;
            memoTable[i][j] = 100000000;
            for (k = i; k < j; k++)
            {
                long ans = memoTable[i][k] + memoTable[k + 1][j] + dim[i - 1] * dim[k] * dim[j];
                if (ans < memoTable[i][j])
                {
                    bestK[i][j] = k;
                    memoTable[i][j] = ans;
                }
            }
        }
    }
    return memoTable[1][matrixNum];
}

int main()
{
    int i, matrixNum;
    while (EOF != scanf("%d", &matrixNum))
    {
        for (i = 0; i <= matrixNum; i++)
            scanf("%d", &dim[i]);
        printf("%ld\n", MatrixChain(matrixNum));
    }
    return 0;
}

矩阵连乘的备忘录算法：

#include <stdio.h>
#include <string.h>
#define MaxNum 1000

long MatrixChainMemo(int i, int j);
int dim[MaxNum];
long memoTable[MaxNum][MaxNum];
int bestK[MaxNum][MaxNum];

long MatrixChainMemo(int, int);

long MatrixChainMemo(int i, int j)
{
    if (memoTable[i][j] != -1)
        return memoTable[i][j];
    if (i == j)
    {
        memoTable[i][j] = 0;
        return 0;
    }
    long ans, min = 100000000;
    for (int k = i; k < j; k++)
    {
        ans = MatrixChainMemo(i, k) + MatrixChainMemo(k + 1, j) + dim[i - 1] * dim[k] * dim[j];
        if (ans < min)
        {
            bestK[i][j] = k;
            min = ans;
        }
    }
    memoTable[i][j] = min;
    return min;
}

int main()
{
    int i, matrixNum;
    memset(memoTable, -1, sizeof(memoTable));
    while (EOF != scanf("%d", &matrixNum))
    {
        for (i = 0; i <= matrixNum; i++)
            scanf("%d", &dim[i]);
        printf("%ld\n", MatrixChainMemo(1, matrixNum));
    }
    return 0;
}

一般来讲，

• 当一个问题的所有子问题至少都要解一次时，自底向上的动态规划算法比自顶向下的备忘录算法效率高。
• 当一个问题的部分子问题不需要求解时，自顶向下的备忘录算法比自底向上的动态规划算法效率高。

最优二叉搜索树

问题描述：设是有序集 $S=\left\{S_{1}, S_{2}, \cdots, S_{n}\right\}$，且 $s_{1}<s_{2}<\cdots<s_{n}$，有序集 $S$ 用二叉搜索树来表示，即 $S$ 中的每一个元素都是二叉搜索树的结点。

二叉搜索树：任意结点中的元素 $s$ 大于其左子树（如果存在）中任一结点所存储的元素，小于其右子树（如果存在）中任一结点所存储的元素。

假设 $S$ 中的元素 $s_{i}$ 被查找的概率为 $p_{i}(0<p_{i}<1)$。可能存在某些查询值不包含在集合 $S$ 中，因此在二叉查找树中设置 $n+1$ 个虚结点 $e_{0}, e_{1}, \cdots, e_{n}$ 表示不在$S$中的那些查询值，每个虚结点被查找的概率为 $q_{i}(0<q_{i}<1)$

• $e_{0}$ 表示小于 $s_{1}$ 的所有值；
• $e_{n}$ 表示大于 $s_{n}$ 的所有值；
• 对于 $i=1,2,...,n-1$，$e_{i}$ 表示在 $(s_{i},s_{i+1})$ 之间的所有值。

这样得到了结点分类：

• $s_{i}$ 实结点（内部结点）：对应查找概率 $p_{i}$
• $e_{i}$ 虚结点（叶子结点）：对应查找概率 $q_{i}$

每次检索要么成功，查询到实结点；要么失败，查询到虚结点。

$\sum_{i=1}^n p_i+\sum_{i=0}^n q_i=1$

对于一个有序集 $S$，可以构造多个二叉搜索树。衡量二叉搜索树的查找效率通常采用平均比较次数作为衡量指标。设在表示 $S=\left\{S_{1}, S_{2}, \cdots, S_{n}\right\}$ 的二叉搜索树 $T$ 中，

• 实结点 $s_{i}$ 的结点深度为 $dp(s_{i})$（根结点的深度为 $0$），查找概率为 $p_{i}$，其中 $1 \leqslant i \leqslant n$；
• 虚结点 $e_{j}$ 的结点深度为 $dp(e_{j})$，查找概率为 $q_{j}$，其中 $0 \leqslant j \leqslant n$；

根据二叉树的特性

• 如果在深度为 $dp(s_{i})$ 的实结点 $s_{i}$ 处查找结束，需要比较次 $dp(s_{i})+1$ 次
• 如果在深度为 $dp(e_{j})$ 的虚结点 $e_{j}$ 处查找结束，需要比较次 $dp(e_{j})$ 次

二叉搜索树 $T$ 的平均比较次数定义为：

$C=\sum_{i=1}^{n} p_{i}\left(\mathrm{dp}\left(s_{i}\right)+1\right)+\sum_{j=1}^{n} q_{j} \operatorname{dp}\left(e_{j}\right)$

最优二叉搜索树：在所有表示有序集 $S$ 的二叉搜索树中，具有最小平均比较次数的二叉搜索树。

现在给定有序集 $S$ 对应的概率 $p_{i}$ 和 $q_{j}$，求解最优二叉搜索树。

输入：

• 多组测试数据，每组数据包含三行
  • 有序集 $S$ 元素的个数 $n(n<1000)$
  • $S$ 中 $n$ 个元素的查找概率 $p$
  • $S$ 中 $n+1$ 个虚结点的查找概率 $q$

输出：

最优二叉树的平均比较次数，保留四位有效数字。每组测试样例输出一行。

问题分析

🔴最优子结构：

• $T(1,n)$：实结点 $\left\{s_{1}, s_{2}, \cdots, s_{n}\right\}$ 和虚结点 $\left\{e_{0}, e_{1}, \cdots, e_{n}\right\}$ 构成的二叉搜索树。

• $T(1,k-1)$：实结点 $\left\{s_{1}, s_{2}, \cdots, s_{k-1}\right\}$ 和虚结点 $\left\{e_{0}, e_{1}, \cdots, e_{k-1}\right\}$ 构成的二叉搜索树——左子树。

• $T(k+1,n)$：实结点 $\left\{s_{k+1}, s_{2}, \cdots, s_{n}\right\}$ 和虚结点 $\left\{e_{k}, e_{k+1}, \cdots, e_{n}\right\}$ 构成的二叉搜索树——右子树。

假设 $T(1,n)$ 是实结点 $\left\{s_{1}, s_{2}, \cdots, s_{n}\right\}$ 和虚结点 $\left\{e_{0}, e_{1}, \cdots, e_{n}\right\}$ 的最优二叉搜索树，那么：

• $T(1,k-1)$：实结点 $\left\{s_{1}, s_{2}, \cdots, s_{k-1}\right\}$ 和虚结点 $\left\{e_{0}, e_{1}, \cdots, e_{k-1}\right\}$ 的最优二叉搜索树。

• $T(k+1,n)$：实结点 $\left\{s_{k+1}, s_{2}, \cdots, s_{n}\right\}$ 和虚结点 $\left\{e_{k}, e_{k+1}, \cdots, e_{n}\right\}$ 的最优二叉搜索树。

⚫状态表示和状态递推方程：

$T(i,j)$：一颗子树通过两个参数确定，开始关键字下标 $i$ 和结束关键字下标 $j$。

$C(i,j)$：子树 $T(i,j)$ 的最优二叉搜索树的平均比较次数。

$C(1,n)$：原问题的最优解。

1. $j=i-1$，空子树，$C(i, j)=0$
2. $j>i-1$，根据最优子结构计算 $C(i,j)$，是三部分的平均比较次数之和：
   1. 根结点$s_{r}$，$i \leqslant r \leqslant j$；
   2. 左子树：$T(i,r-1)$；
   3. 右子树：$T(r+1,j)$。

当一颗二叉树成为一个结点的子树时，则子树中每个结点的深度加 $1$，该子树的平均比较次数增加一个量——子树所有关键字的概率之和。即：

• 树 $T(i,r-1)$ 成为根结点 $s_r$ 的左子树：$C^{\prime}(i, r-1)=C(i, r-1)+\sum_{k=i}^{r-1} p_{k}+\sum_{k=i-1}^{r-1} q_{k}$
• 树 $T(r+1,j)$ 成为根结点 $s_r$ 的右子树：$C^{\prime}(r+1, j)=C(r+1, j)+\sum_{k=r+1}^{j} p_{k}+\sum_{k=r}^{j} q_{k}$
• 根结点的平均比较次数为 $p_r$

$\begin{aligned}C(i, j) &=C^{\prime}(i, r-1)+C^{\prime}(r+1, j)+p_{r} \\&=C(i, r-1)+\sum_{k=i}^{r-1} p_{k}+\sum_{k=i-1}^{r-1} q_{k}+C(r+1, j)+\sum_{k=r+1}^{r-j} p_{k}+\sum_{k=r}^{j} q_{k}+p_{r} \\&=C(i, r-1)+C(r+1, j)+\sum_{k=i}^{j} p_{k}+\sum_{k=i-1}^{j} q_{k}\end{aligned}$

令 $\omega(i, j)=\sum_{k=i}^{j} p_{k}+\sum_{k=i-1}^{j} q_{k}$

最终表示为：

$C(i, j)=C(i, r-1)+C(r+1, j)+\omega(i, j)$

又最优二叉搜索树的根结点无法事先确定，我们枚举所有可能的根结点 $s_{r}$, $i \leqslant r \leqslant j$，并统计最小的平均比较次数，因此 $C(i,j)$ 的状态转移方程为：

$C(i, j)= \begin{cases}0, & j=i-1 \\ \omega(i, j)+\min _{i \leqslant r \leqslant j}\{C(i, r-1)+C(r+1, j)\}, & i \leqslant j\end{cases}$

🔵计算最优值

算法实现与分析

#include <stdio.h>
#include <string.h>
#define MaxNum 1000

double C[MaxNum][MaxNum], root[MaxNum][MaxNum];
double w[MaxNum][MaxNum];

double OptimalBST(double *p, double *q, int n);

double OptimalBST(double *p, double *q, int n)
{
    int i, j, r, k;
    for (i = 0; i < n; i++)
    {
        w[i + 1][i] = q[i];
        C[i + 1][i] = 0;
    }
    for (r = 0; r < n; r++)
    {
        for (i = 1; i <= n - r; i++)
        {
            j = i + r;
            w[i][j] = w[i][j - 1] + p[j] + q[j];
            C[i][j] = C[i + 1][j];
            root[i][j] = i;
            for (k = i + 1; k <= j; k++)
            {
                double dTemp = C[i][k - 1] + C[k + 1][j];
                if (dTemp < C[i][j])
                {
                    C[i][j] = dTemp;
                    root[i][j] = k;
                }
            }
            C[i][j] += w[i][j];
        }
    }
    return C[1][n];
}

int main()
{
    int n;
    double pProb[MaxNum], qProb[MaxNum];
    while (EOF != scanf("%d", &n))
    {
        for (int i = 1; i <= n; i++)
            scanf("%lf", &pProb[i]);
        for (int i = 0; i <= n; i++)
            scanf("%lf", &qProb[i]);
        printf("%1.4lf\n", OptimalBST(pProb, qProb, n));
    }
    return 0;
}

多段图最短路径

问题分析

算法设计与实现

最长公共子序列

问题描述：若给定序列 $X=\left\{x_{1}, x_{2}, \cdots, x_{m}\right\}$，$Z=\left\{z_{1}, z_{2}, \cdots, z_{k}\right\}$，若$Z$是$X$的子序列，当且仅当存在一个严格递增下标序列 $\left\{i_{1}, i_{2}, \cdots, i_{k}\right\}$，使得对于所有 $j=1,2,...,j$ 有：$z_{j}=x_{i_{j}}$

举例：$Z=\{B, C, D, B\}$ 是 $X=\{A, B, C, B, D, A, B\}$ 的子序列，相应的递增下标序列为$\{2,3,5,7\}$

• $z_{1}=x_{2}=B$
• $z_{2}=x_{3}=C$
• $z_{3}=x_{5}=D$
• $z_{4}=x_{7}=B$

$\left\{i_{1}, i_{2}, \cdots, i_{k}\right\}$ = $\{2,3,5,7\}$

给定序列 $X$ 和序列 $Y$，当序列 $Z$ 既是 $X$ 的子序列又是 $Y$ 的子序列，称 $Z$ 是序列 $X$ 和序列 $Y$ 的公共子序列。其中在这些公共子序列中，包含元素最多的序列称为最长公共子序列。任意给定两个字符序列 $X=\left\{x_{1}, x_{2}, \cdots, x_{m}\right\}$ 和 $Y=\left\{y_{1}, y_{2}, \cdots, y_{n}\right\}$，设计算法求解它们的最长公共序列。

输入：

• 包含多组测试数据
• 第一行输入字符序列 $X$
• 第二行输入字符序列 $Y$
• $X$ 和 $Y$ 的字符长度不大于1000000

输出：最长公共子序列的长度，每组测试数据输出一行。

问题分析

🔴最优子结构：设序列 $X=\left\{x_{1}, x_{2}, \cdots, x_{m}\right\}$ 和 $Y=\left\{y_{1}, y_{2}, \cdots, y_{n}\right\}$ 的最长公共子序列为 $Z=\left\{z_{1}, z_{2}, \cdots, z_{k}\right\}$，那么以下结论成立：

1. 若 $x_{m}=y_{n}$，则 $z_{k}=x_{m}=y_{n}$，且 $Z_{k-1}=\left\{z_{1}, z_{2}, \cdots, z_{k-1}\right\}$ 是 $X_{m-1}=\left\{x_{1}, x_{2}, \cdots, x_{m-1}\right\}$ 和 $Y_{n-1}=\left\{y_{1}, y_{2}, \cdots, y_{n-1}\right\}$ 的最长公共子序列；
2. 若 $x_{m} \neq y_{n}$ 且 $z_{k}\neq x_{m}$，则 $Z$ 是 $X_{m-1}$ 和 $Y$ 的最长公共子序列；
3. 若 $x_{m} \neq y_{n}$ 且 $z_{k} \neq y_{n}$，则 $Z$ 是 $X$ 和 $Y_{n-1}$ 的最长公共子序列。

⚫状态表示和状态递推方程：$C(i, j)$：序列 $X_{i}=\left\{x_{1}, x_{2}, \cdots, x_{i}\right\}$ 和 $Y_{j}=\left\{y_{1}, y_{2}, \cdots, y_{j}\right\}$ 的最长公共子序列长度。

• 当 $i=0$ 或 $j=0$ 时，其中一个序列为空串，没有公共子序列，$C(0,0)=0$
• 当 $i,j>0$ 时，类似与最优子结构分析
  • $x_{i}=y_{j}$ 时，$C(i, j)=C(i-1, j-1)+1$
  • $x_{i} \neq y_{j}$ 时，$C(i, j)=max(C(i-1,j),C(i,j-1))$，分解为两个子问题
    • $\left(X_{i-1}, Y_{j}\right)$的最长公共子序列
    • $\left(X_{i}, Y_{j-1}\right)$的最长公共子序列

综上所述，$C(i,j)$的递推方程如下：

$C(x, y)=\left\{\begin{array}{ll}0, & i=0, j=0 \\C(i-1, j-1)+1, & i, j>0, x_{i}=y_{j} \\\max \{C(i-1, j), C(i, j-1)\}, & i, j>0, x_{i} \neq y_{j}\end{array}\right.$

🔵计算最优值：

二维数组 $C[i][j]$：记录 $X_{i}=\left\{x_{1}, x_{2}, \cdots, x_{i}\right\}$ 和 $Y_{j}=\left\{y_{1}, y_{2}, \cdots, y_{j}\right\}$ 的最长公共子序列长度。

二维数组 $B[i][j]$：记录 $C[i][j]$ 的值是由哪一个子问题的解得到的

• $B[i][j]=1$，表示 $C[i][j]$ 的值 $C[i-1][j-1]$ 得到的；
• $B[i][j]=2$，表示$C[i][j]$的值 $C[i-1][j]$ 得到的；
• $B[i][j]=3$，表示$C[i][j]$的值 $C[i][j-1]$ 得到的。

1. 输入序列为空的情形，$C(i,0)=0$，$C(0,j)=0$，对应数组 $C$ 的第一行和第一列。
2. 计算
   1. $i=1$，$j=1,2,...,m$ 时，$C(i,j)$ 的值；
   2. $i=2$，$j=1,2,...,m$ 时，$C(i,j)$ 的值；
   3. $\cdots$
   4. $i=n$，$j=1,2,...,m$ 时，$C(i,j)$ 的值。
3. 依次填充 $C[i][j]$ 的值。

算法实现与分析

#include <stdio.h>
#include <string.h>
#define MAX 100

int lcsLength(char *, char *);

int lcsLength(char *strX, char *strY)
{
    int C[MAX][MAX], B[MAX][MAX], i, j;
    int m = strlen(strX) + 1;
    int n = strlen(strY) + 1;
    for (i = 0; i < m; i++)
        C[i][0] = 0;
    for (j = 0; j < n; j++)
        C[0][j] = 0;
    for (i = 1; i < m; i++)
    {
        for (j = 1; j < n; j++)
        {
            if (strX[i - 1] == strY[j - 1])
            {
                C[i][j] = C[i - 1][j - 1] + 1;
                B[i][j] = 1;
            }
            else if (C[i - 1][j] >= C[i][j - 1])
            {
                C[i][j] = C[i - 1][j];
                B[i][j] = 2;
            }
            else
            {
                C[i][j] = C[i][j - 1];
                B[i][j] = 3;
            }
        }
    }
    return C[m - 1][n - 1];
}

int main()
{
    char strX[MAX], strY[MAX];

    while (EOF != scanf("%s%s", strX, strY))
    {
        int ans = lcsLength(strX, strY);
        printf("%d\n", ans);
    }
    return 0;
}

0-1 背包问题

问题分析

算法实现与分析

#include <cstdio>
#include <cstring>
#define MaxN 1000
#define MaxC 1000

int n, C;
int w[MaxN];
double v[MaxN];
double Val[MaxC];

double binaryKnapsack(int, int *, double *, int);

double binaryKnapsack(int numItems, int *w, double *v, int capacity)
{
    memset(Val, 0, sizeof(Val));
    for (int i = 0; i < numItems; i++)
        for (int j = capacity; j >= 0; j--)
            if (j >= w[i] && Val[j] < Val[j - w[i]] + v[i])
                Val[j] = Val[j - w[i]] + v[i];
    return Val[capacity];
}

int main()
{

    while (scanf("%d%d", &n, &C) != EOF)
    {
        for (int i = 0; i < n; i++)
            scanf("%d", &w[i]);
        for (int i = 0; i < n; i++)
            scanf("%lf", &v[i]);
        double ans = binaryKnapsack(n, w, v, C);
        printf("%. 1f\n", ans);
        return 0;
    }
}

最大上升子序列

问题分析

算法实现与分析